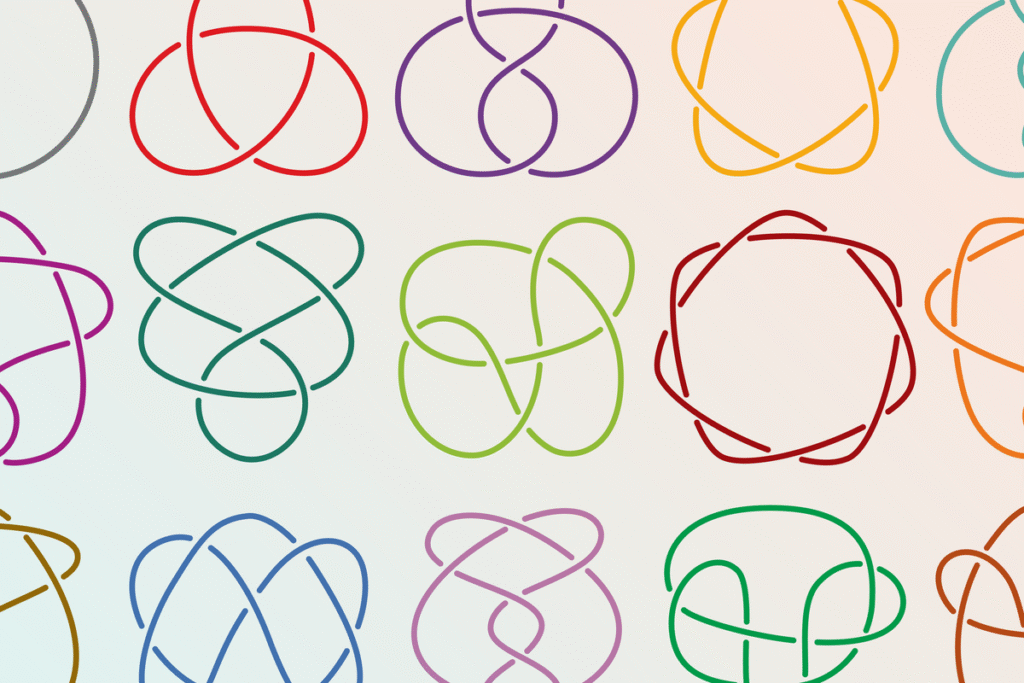Find a string. Really. Do it. Now twist, tie and tangle it as much as you like. Finally, attach the two loose ends of your string together to make a closed loop. (This is a crucial step.) What you hold in your hands is one of the most exciting mathematical objects of the 20th century: a knot. (Hopefully you didn’t use your headphone wire.)
Which knot in each of the following pairs can be unraveled into a circle without opening the loop?
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
In pair 1, the knot on the left completely unravels, and in pair 2, the knot on the right does so.
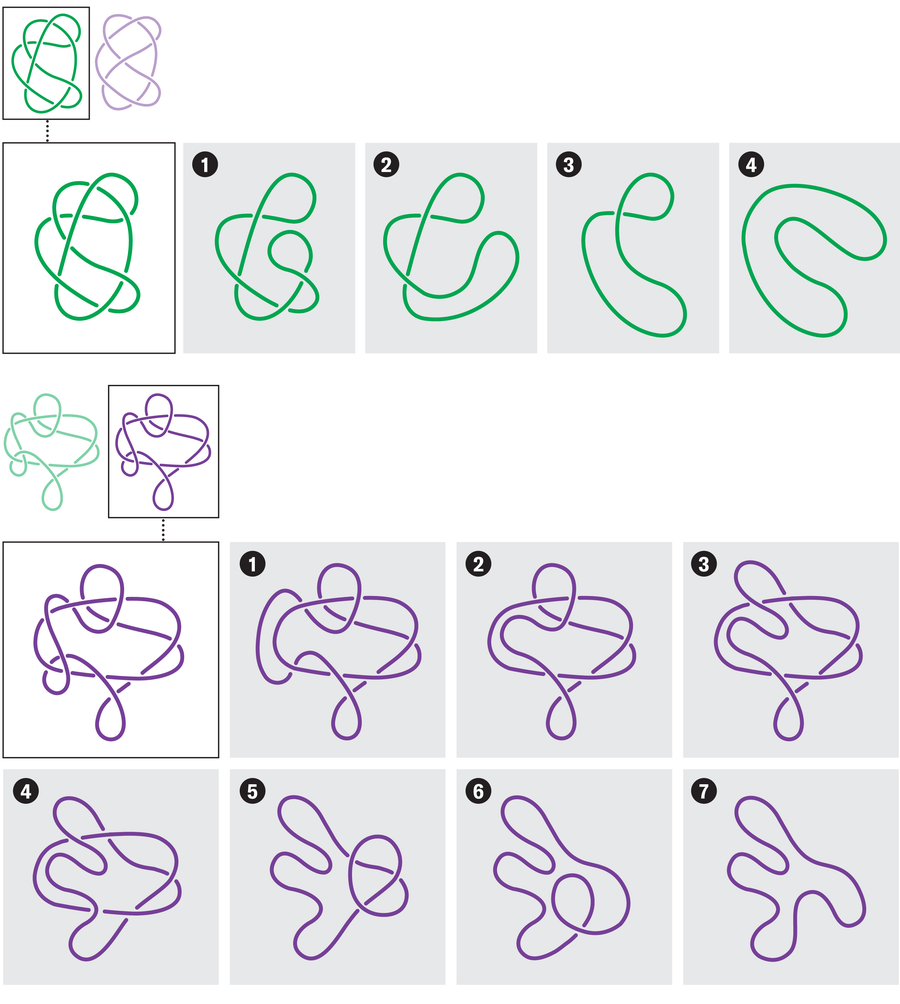
Graphic shows how to undo the first knot from pair 1 in four steps and the second knot from pair 2 in seven steps.
A bonus challenge: the other two knots can be rearranged to look like two others pictured in this article. Can you find them? (See the answer in our September issue puzzle.)
Any knot that can be unraveled into a circle, as two of the above can, is equivalent to the delightfully named unknot. But what about the other two knots? How could we possibly be sure that no amount of pulling, twisting and tying could turn them into circles without wearing out our headphone wires? Is there a way to know that they’re really two different knots—that they can’t be arranged to look identical to each other? These are some of the fundamental questions in the mathematical field of knot theory.
Humans have been tying knots since prehistoric times for their practicality and beauty. Mathematical knots, in particular—knots with attached ends—show up as a recurring motif in Chinese and Celtic artwork that dates back centuries.

But the mathematical classification of knots didn’t begin until the 1870s. Researchers who created early tables that categorized different knots were driven by the idea that atoms were knotted vortices. They reasoned that by tabulating all possible knots, they could make a periodic table of elements. These chemical efforts were spearheaded in part by Lord Kelvin (creator of the eponymous temperature scale). Even after chemists discovered that atoms aren’t actually knots, mathematicians ran with the idea, forming an entire branch of study around the tricky creatures.
Mathematicians typically manipulate knots through diagrams like these:
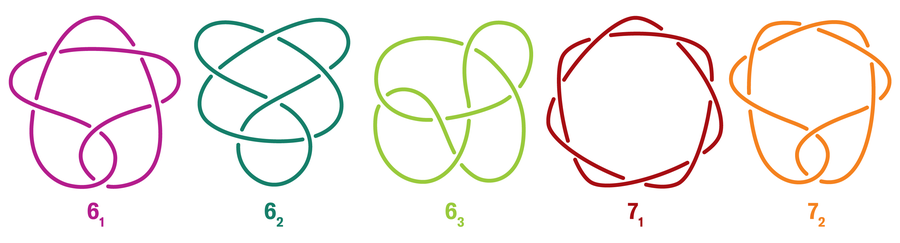
(But we do still pull out physical string now and again.) Each place where one strand passes over another in a knot diagram is called a crossing. An unknot (also known as the trivial knot) can be drawn with any number of crossings. Here are unknots with 7, 11 and 15:
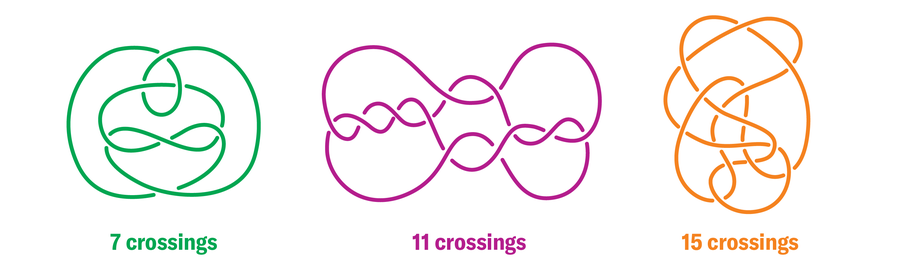
What is the smallest number of crossings you can use to craft a knot that is not trivial? Draw it.
We can see that any knot diagram with only one crossing will be an unknot. Starting with a drawing of just a crossing, we can test all the possible ways of connecting the ends together without crossing them over each other. Then we can see that all of these are the unknot. We can do something similar to see that there are no nontrivial knot diagrams with two crossings.
But can a nontrivial knot have three crossings? Yes! There’s exactly one (and its mirror image), and it’s called the trefoil knot. We’ll show that the trefoil knot can’t be manipulated into a simple circle down below.
Any possible manipulation of a knot diagram that does not fundamentally change the knot can be achieved by a series of three operations called Reidemeister moves. They include taking a strand and adding or subtracting a twist, sliding one strand over or under another, and passing a strand under, over or in between two strands in a crossing:
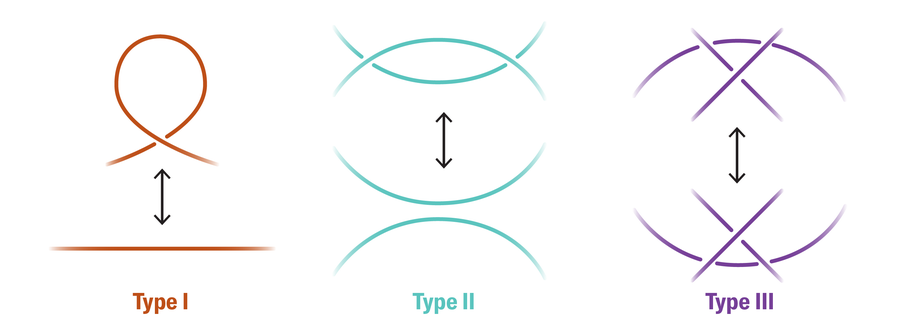
Any characteristic of a knot that doesn’t change when rearranged in this way is called a “knot invariant.” Take, for example, tricolorability. A knot is tricolorable if each arc in a diagram of that knot can be assigned a different color according to the following rules:
-
At each crossing, all three segments are either the same color or different colors.
-
Multiple colors are used.

A standard unknot, represented as a circle, certainly isn’t tricolorable. There’s only one arc, so it’s impossible to satisfy rule #2. But what if we use different diagrams of the unknot, as above?
Using Reidemeister moves to represent all possible things you can do to a knot diagram, show that tricolorability really doesn’t depend on how you draw the diagram.
Here’s how to show that Reidemeister II moves, for example, don’t affect tricolorability. First we examine all the ways the arcs involved in the RII move can be tricolored (up to switching which color is which). Then we show that they can still be colored in a way that doesn’t break the rules and preserves the colors of the strands that connect back to the rest of the knot when the move is performed.
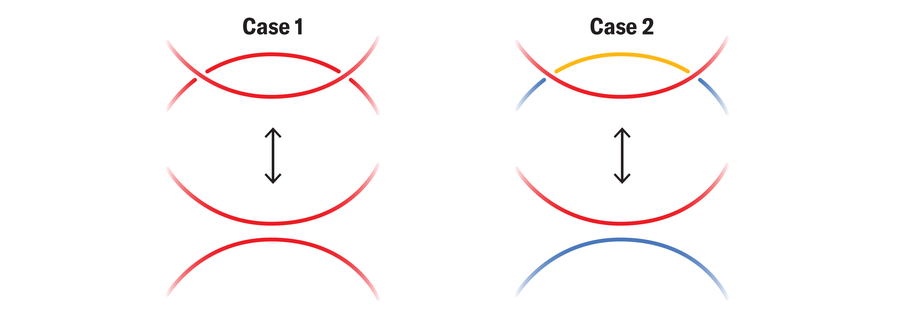
A similar argument will work for the RI move, which will require fewer cases, and for the RIII move, which will require many more.
Show that the “trefoil knot” below is tricolorable and therefore not equivalent to the unknot.

Here is one way of tricoloring the trefoil knot. As is necessary, at every crossing, the strands are either all the same color or all different, and all three colors have been used. (In this case, all the strands are different colors at each crossing.)

Not all knots can be distinguished using tricolorability.
Show that no matter what coloring you use, this figure-eight knot, like the unknot, is not tricolorable:
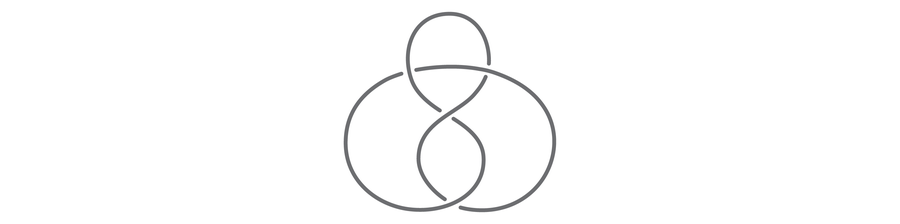
Just showing that one way of coloring the figure-eight knot isn’t a tricoloring won’t be enough to show it isn’t possible, so we have to make sure we cover all possible colorings. Start by choosing a color for the arc at the top. Whether this strand in particular is red or yellow or blue does not change the proof, so we can let it be red “without loss of generality.” Now we can break the problem into two cases. The arc on the right can either be the same color or a different color than the one on top.
Case 1: Suppose the arc on the right is also red. The top arc and the right arc meet at a crossing with the left arc, so to follow the rules, the left arc must also be red. In the same way, the 4th and middle arc must also be red. Now the whole knot is colored and not all 3 colors have been used, so this is not a valid tricoloring.
Case 2: Now let the arc on the right be a different color than the top one. The argument is the same if we let it be blue or yellow, so again, “without loss of generality,” let it be blue. Now the red arc and the blue arc meet the left arc at a crossing, so to follow the rules, the left arc must be yellow. The blue and red arc meet the center arc at a crossing, so it must be yellow. But the blue and yellow arcs also meet it at a crossing, so it can’t be yellow. There’s no choice of color for the center arc that would not break the tricoloring rules.

Thus we have shown that no matter what we try, the figure-eight knot is not tricolorable.
For any given knot, there are only two options: either it is tricolorable or it isn’t. We say, then, that tricolorability assigns each knot a yes or no value. But more complex knot invariants can assign each knot a number, a polynomial or even a mathematical object called a group. The crossing number of a knot, for example, is the smallest number of crossings it can be drawn with. The unknotting number is the smallest number of crossing changes (rearrangements of strand order in a particular crossing, as shown below) needed to transform a knot into the unknot. The trefoil knot has unknotting number 1.
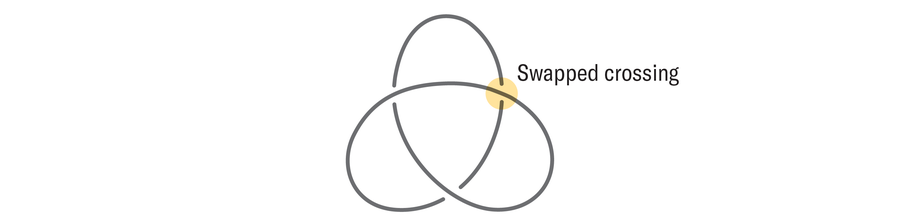
Take a guess at the unknotting number of the following knots:

The figure-eight knot on the left has unknotting number 1. The knot in the middle, sometimes called the cinquefoil knot, has unknotting number 2. The knot on the right has unknotting number 3. These unknotting numbers are impossible to prove without some more complex tools; we must show there is no diagram of these knots in which they can be unknotted in fewer crossing changes.
The diagram on the right above shows a figure-eight knot connected to a cinquefoil in what is called a “connected sum.” It was long believed that the unknotting number of the connected sum of two knots was the sum of their individual unknotting numbers. In this case, that’s true—the unknotting number of the third knot is 1 + 2 = 3. But in a recent twist of events, it was shown this is not always the case.
A knot that cannot be described as a connected sum of two other (nontrivial) knots is called a “prime knot,” and, just as prime numbers are the building blocks of positive integers, these knots make up the structure of all other knots. Prime knots are listed in standard knot tables like this one inspired by early knot tabulators such as Lord Kelvin:
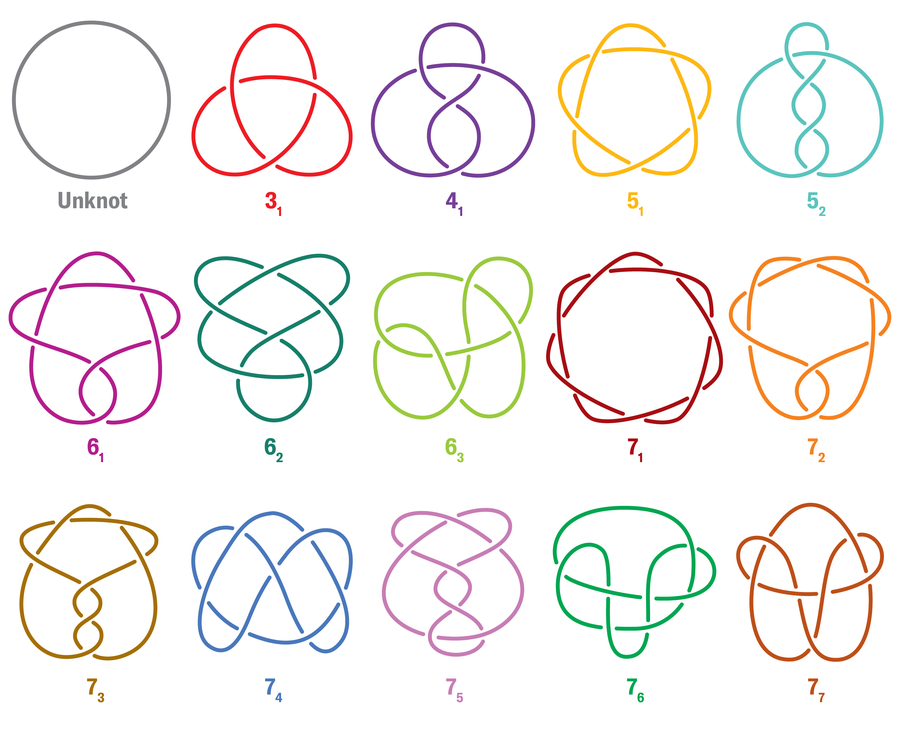
The cinquefoil we saw above is officially dubbed 51, which means its crossing number is 5 and it is the first one with that crossing number listed in the standard knot table. So far, mathematicians have managed to tabulate all prime knots of up to crossing number 20. (For a sense of scale, there are 1,847,319,428 prime knots with crossing number 20, excluding mirror images.)
The mathematics of knot theory can also be used to study links, which are interconnected knots. Instead of one loop knotted up in space, links can contain any number of knotted components linked together.
Here’s an example of a link whose components are all unknots:

This link is known as the “Borromean rings,” and it has an interesting property. All three of the loops are linked (that is, they can’t be separated out from the others without cutting), but no two components are linked together independently: removing any one of the rings leaves the remaining ones unlinked.
Can you find a four-component link with this same property? None of the four components can be separated out, but removing one will separate all the remaining ones.
Here’s another drawing of the Borromean rings. Can you think of a way to extend the pattern?

Using the format of the hint above we can draw the following four-component version of the Borromean rings, known as the four-component Brunnian link.
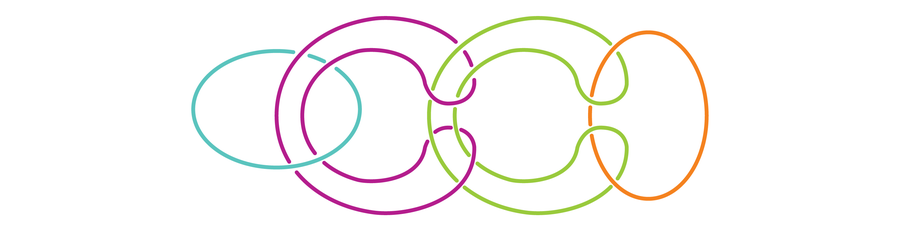
It can also be rearranged to look like this:

Or it can form any number of other pictures. As long as all of your components are linked together and removing any one will unlink them all, you’ve got the right answer!
The leap from knots to links is a relatively small one, but mathematicians can extend the ideas of knot theory to study mind-bending concepts such as higher-dimensional knots, surfaces with knotted edges and difficult-to-imagine objects obtained by subtracting a knot from three-dimensional space.
And although chemists set knots aside as a way to describe atoms, they now use knot theory to examine the structures of different molecules and synthesize new materials. Biologists use it, too, to understand the way proteins in our cells tangle up and to create effective gene-editing technologies. These are just more examples of how mathematics and the sciences play off of each other to help us better understand the inner workings of the universe. Happy knotting!