Everyone makes mistakes—and sometimes those mistakes can lead to surprising discoveries. In the early 1990s, while programming the computer game Doom, game developer John Carmack set the value of pi (π) by hand—and in true nerd fashion, he wrote the number down to the ninth decimal place from memory: 3.141592657.
Do you notice anything strange about that figure? The last digit is wrong. The number should instead be 3.141592654. (Pi is often truncated without rounding, in which case the ninth decimal place would be filled by 3, but it rounds to 4 because the subsequent digit is 5.)
Fortunately, this error has little impact on the game. In Doom, one of the earliest first-person shooters with three-dimensional graphics, you take on the role of a space marine who, because of a failed teleportation experiment, ends up on a moon of Mars, where he fights demons and zombies. The game has a great story but terrible graphics. That’s not because of the incorrect pi value but rather a reflection of how little computing power was available in the 1990s.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Still, the error inspired U.S. engineer Luke Gotszling to investigate the possible consequences of incorrectly programming pi at a larger scale in the game—an idea he presented at a hackers conference in 2022.
When Pi Is Wrong in a Computer Game
Because Doom is an open-source computer game, you can download the code—and modify it. Gotszling did just that, testing what would happen if he changed the programmed values of pi.
The results can make a viewer feel a bit nauseous. When Gotszling set π = 3, for example, the pixelated world of Doom became distorted, with walls and pillars moving in unexpected ways. Nevertheless, the game was playable.
When pi was set to the value of Euler’s number, 2.718…, the strangeness intensified. As a player moved straight in the game world, surrounding objects would move to different sides. Enemies could appear out of nowhere and disappear again. “With enough intoxication, you can re-create this,” Gotszling joked in his presentation.
Things got really bad when he set a value of π⁄2 for pi. Walls would flash and disappear. Invisible obstacles block the player’s movement. The game wasn’t particularly fun in this state.
Pi Isn’t Always 3.14159…
Why is pi so powerful? To answer that, we need to think about the consequences of changing pi more deeply.
Originally, pi was defined as the ratio of a circle’s circumference to its diameter. In our everyday world, we assume circles are round. But in the narrower mathematical sense, a circle is defined by all points that are equidistant from a common center. In a flat, two-dimensional world, where distances are defined as the shortest straight lines, a circle is round. That means pi’s value can change.
For example, imagine you’re standing in downtown Manhattan. If you want to find out which places are exactly one kilometer away from you, the shape you can create will no longer be round. That’s because you can’t walk through walls. Instead you have to follow the checkerboard layout of the streets. A circle has a square shape in the “Manhattan metric,” as it’s called in mathematical jargon. And if you define pi in this context as the ratio of circumference to diameter, the number takes on completely different values: in the Manhattan metric, pi is exactly 4.
If you look closely, the value of pi in our world isn’t exactly 3.14159…. Instead, the ratio of circumference to diameter takes on a different value—and, worse still, this value varies!
If you are standing at the North Pole and looking at all the places exactly 1,000 kilometers away from you, for instance, these points form a circle on the surface of a sphere—but its circumference is smaller than that of a circle on a flat surface, thanks to the curvature of Earth. The closer you get to the equator, the stronger this effect becomes, and the corresponding value of pi deviates more and more from the usual 3.14159….
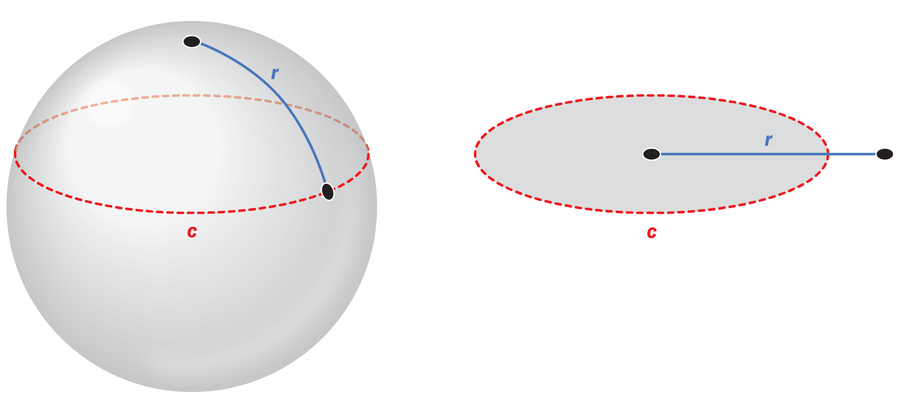
The new value of pi is therefore not constant but instead depends on the radius of the circle. And this isn’t just the case when considering a spherical surface. Any type of curved surface yields variable values for pi.
Mathematicians refer to such curved worlds as “non-Euclidean” geometries. (More than 2,000 years ago, the scholar Euclid laid out the rules of geometry most of us learned in school—ideas that only apply on a flat world.)
Creating a Trippy Vision of Doom
The quirky landscape Gotszling created by tweaking Doom’s source code is something else entirely. To understand it, we have to go back to the 1990s: a time when every arithmetic operation consumed a huge amount of resources. To manage that challenge, programmers made efforts to determine possible calculations in advance and store them in “lookup tables.”
When developing 3D graphics for a computer game, trigonometric functions such as sine, cosine and tangent play an important role. They can be used to describe how objects move through space over time. To save processing power, Doom’s developers calculated important values of the trigonometric functions for various angles in advance and stored them in the lookup tables. And this is where pi comes into play: you have to multiply an angle in degrees by pi to get the corresponding value in radians, which the computer uses.
So if Gotszling used a value of pi that was too small, the angles would be converted incorrectly. Because developers only store a finite number of angles, he created lookup tables with values that no longer include the full rotations: Instead of describing an environment in which an object only reappears in the same place after a 360-degree rotation, this occurs after a significantly smaller angle. As a result, in extreme situations, objects suddenly disappear or reappear out of nowhere.
The Doom world Gotszling has created is incredibly strange. Nevertheless, it’s a nice way to get people thinking about mathematics and the value—in every sense—of pi. One small mistake by a game developer has sparked a much larger experiment into the strange circle number.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

