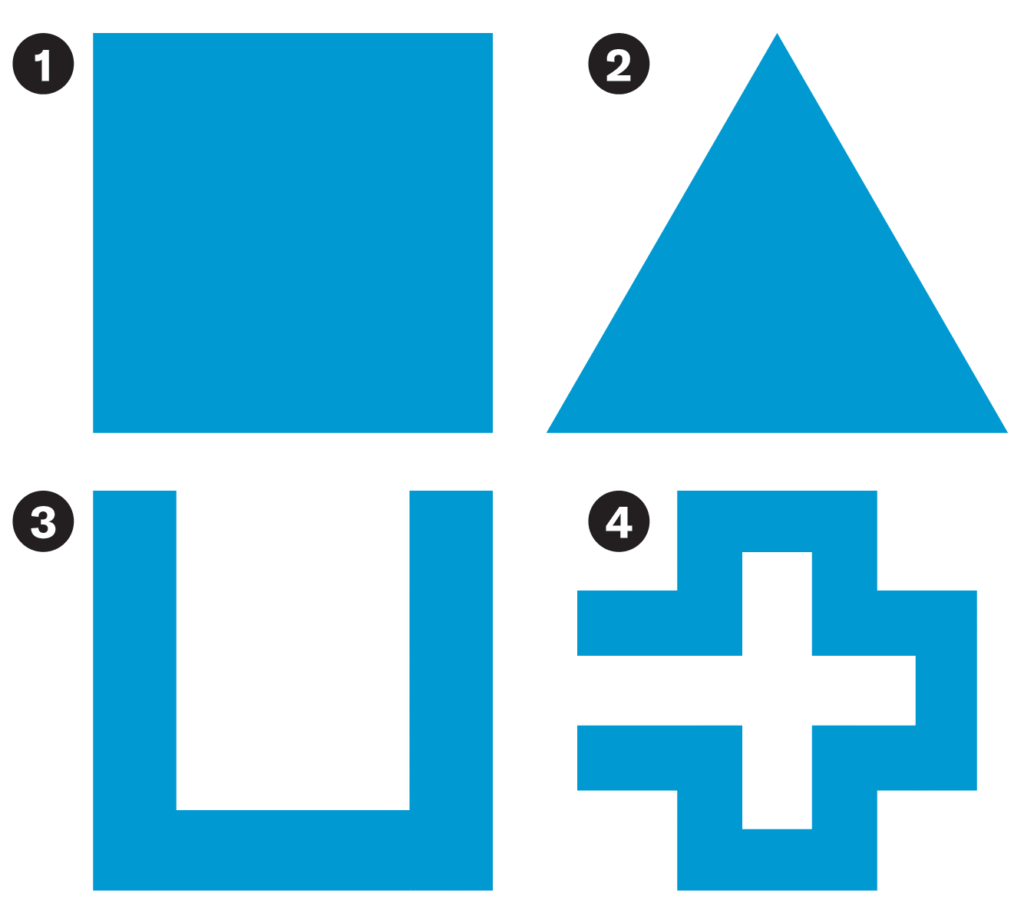
Some say the reason most manhole covers are round is that a circle cannot fall through a smaller circular hole. Which of these other two-dimensional shapes cannot fall through a hole that is the same shape but slightly smaller?
Shapes 1, 2 and 3 can all fall through their own holes. Shape 4 cannot.
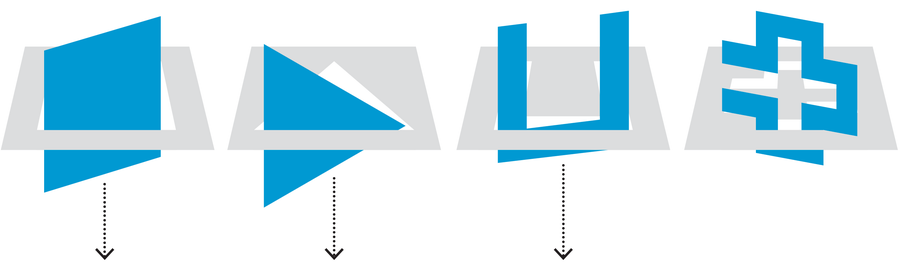
Challenge problem: Can you find another shape that cannot fall through a slightly smaller hole of the same shape?
The circle is one of an infinite family of shapes that have a constant diameter—that is, no matter what angle a line crosses it at, the widest point of the shape will always be the same. The Reuleaux triangle is another example and thus another shape that cannot fall through a slightly smaller hole of the same shape.
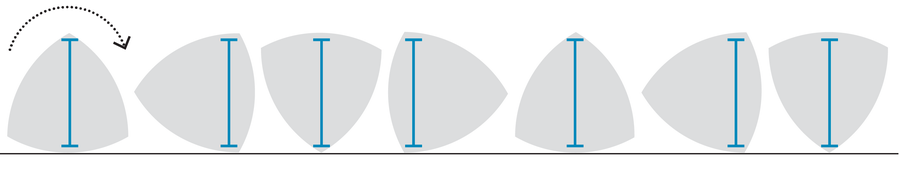
You could also find a shape similar to number 4 whose individual straight segments are smaller than the smallest diameter of the shape.
Shapes that can fall through a hole in another copy of the same shape are known as “Rupert.” Read more here about the recent discovery of the “noperthedron,” the first provably non-Rupert shape of its kind.
We’d love to hear from you! E-mail us at games@sciam.com to share your experience.