A molecularly impermeable polymer from two-dimensional polyaramids

Materials

TMC, melamine and N-Methyl-2-pyrrolidone (NMP) were open and stored in a N₂-environment glovebox. All other reagents, including acetone, isopropyl alcohol (IPA), TFA, deuterated TFA, polystyrene (280 kDa), anisole, chloroform, hexane, dimethyl formamide and DMSO were obtained from commercial vendors and used as received. CD-flat holey carbon (8/2-hole pattern) grids used for TEM were purchased from Electron Microscopy Sciences.

Synthesis of 2DPA-1 powder

For a typical 2DPA-1 powder with a high r value, we first mix 1 mmol of TMC with 1 mmol of melamine in a 40-ml glass vial. Using a magnetic stir bar, stir the contents in a N₂-environment glovebox with 18 ml of NMP followed by 2 ml of pyridine. Seal the glass vial with a solvent-resistant cap, and leave the reaction mixture to stir between 350 rpm and 400 rpm at room temperature inside the glovebox for 24 h. The r value can be manipulated by altering the duration the reaction mixture is left stirring. After the desired stir time has passed, add 20 ml of IPA into the reaction vial and let the vial continue stirring for 30 min to fully quench the reaction. Remove the vial from the glovebox, add 20 ml of deionized water, and filter the reaction mixture using a nylon membrane (Cytiva nylon membrane filters, 0.45-μm pore size, diameter 47 mm, product no. 7404-004) and then wash the solid residue repeatedly with IPA. Collect the IPA-rinsed solid residue from the filter paper and place in a clean 20-ml glass vial. Add 10 ml of deionized water and 10 ml of acetone (1:1 volume ratio) into the vial, and stir the solution with a magnetic stir bar for at least 8 h at room temperature. This helps dissolve any remaining impurities. After 8 h, filter the mixture again with a plastic filter funnel (Chemglass Life Sciences filter funnel, disposable, 110 ml, 10 μm polyethylene frit, product no. OP-6602-14), and wash the solid residue several times with acetone. Collect the solid from the filter and dry in a vacuum oven at 100 °C for 3 h. The resulting powder should possess a yellow to light orange hue.

Characterization methods for bulk 2DPA-1 and thin films

Characterizing 2DPA-1 samples with nuclear magnetic resonance (NMR) spectroscopy followed previously established protocol³⁸. In brief, we first suspended 2DPA-1 powders in TFA at a concentration of 10 mg ml⁻¹. We sonicated the solution in a Branson ultrasonic cleaner for 15 min before adding into a Wilmad NMR tube (5 mm diameter, economy). All the ¹H NMR measurements were performed at room temperature on an Avance III HD 500 NMR Bruker spectrometer with D1 setting of 1 s. Characterization by means of ¹³C NMR is reported elsewhere³⁸.

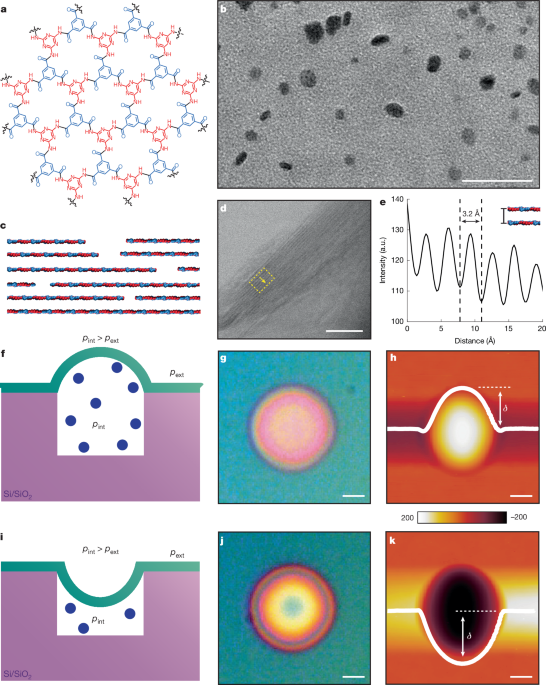
TEM imaging was conducted using S/TEM (Titan Themis Z G3 Cs-Corrected S/TEM) in the TEM mode with an accelerating voltage of 200 kV. Images were taken at magnifications ranging from ×11,000 to ×4,000,000 using the fast 4k × 4k complementary metal-oxide-semiconductor camera at MIT.nano. For TEM sample preparation of nanoplatelets, a diluted solution of 2DPA-1 dissolved in DMSO was drop-cast onto a single-graphene-layer TEM grid. For TEM sample preparation of nanofilms, the as-synthesized 2DPA-1 platelets were initially dissolved in TFA at a concentration of 10 mg ml⁻¹ and then spin-coated onto a TEM grid at 1,000 rpm for 1 min. Both sample types were placed in a vacuum oven at 100 °C overnight to remove TFA and DMSO before TEM analysis.

The chemical stability of 2DPA-1 is imparted by the irreversible nature of its amide bonds having a high dissociation energy. Transamidation, a potential side reaction common to many polyaramids^45,46, is not observed for 2DPA-1 when exposed to TFA for 9 h (ref. ³⁸). Marginal changes in the chemical structure occur after sitting in TFA for 24 h, indicating that some transamidation can occur if the sample remains in highly acidic conditions for an extended period, but this is beyond the exposure that 2DPA-1 would experience before film processing.

One-dimensional polyaramids are notoriously hygroscopic⁴⁷. Using ¹H NMR, we find no notable effect of water on the chemical or molecular structure of 2DPA-1 after 539 d (about 1.5 years) of exposure (Supplementary Fig. 1). The data depict a slight increase in the r value from 5.15 to 5.45 after long-term exposure. The aromatic region and end group region also showed sharp peaks before water storage. Both observations indicate the presence of small particles before water storage, which may have disappeared because of particle aggregation or sedimentation. These data support the chemical stability of this material in protic polar solvents and the lack of hygroscopic degradation observed by the sustained gas barrier properties over 1,000 d in ambient humidity conditions.

Spectroscopy of bulk 2DPA-1 and thin films

Amide linkages for bulk 2DPA-1 and thin films were characterized by means of attenuated total reflectance Fourier transform infrared (ATR-FTIR) and Raman spectroscopy. ATR-FTIR spectra were measured using a Bruker ATR-FTIR Spectrometer with a reflection diamond ATR module. Bulk samples consisted of 2DPA-1 powder compressed against the diamond ATR module with a copper film backing. To obtain infrared signals from the 35-nm 2DPA-1 films used in this study, three films were transferred sequentially onto copper film substrates (thickness about 100 nm) to maximize both sample cross-section and reflectance.

Raman spectra (Supplementary Fig. 2a) were measured using a confocal micro-Raman spectrometer in backscattering geometry equipped with 532-nm and 785-nm laser lines (Horiba LabRAM HR Evolution with hole 500 μm, slit 150 μm, Olympus LMPLFLN ×50 air objective, numerical aperture = 0.5). Low laser powers (about 0.1 mW) were applied to collect spectra with minimal beam damage at 120-s acquisition time over two accumulations. The 785-nm laser was used to detect Raman scattering responses with minimized background photoluminescence. Bulk 2DPA-1 samples were prepared by drop-casting 5 mg ml⁻¹ 2DPA-1 dissolved in TFA onto a SiO₂ substrate. For thin films, we transferred the 35-nm 2DPA-1 film onto a gold-sputtered, surface-enhanced Raman scattering (SERS) substrate to maximize signal. Photoluminescence of 35-nm 2DPA-1 films suspended on the gold SERS substrate was measured using the polarized 532-nm laser line in the Horiba LabRAM. Photoluminescence spectra were collected in normal and parallel modes to assess anisotropy in the molecular ordering of 2DPA-1. In other words, photoluminescence of the film was collected with the excitation source orthogonal and parallel to the film surface by rotating the substrate 90° from lying flat to on-edge, respectively, as described previously⁸.

We performed a normal mode analysis on the vibrational density of states for peak assignment of the simulated structure (Supplementary Table 1). Specifically, we computed the Fourier transforms of the autocorrelation functions of the polarizability tensor¹ and dipole moment vector² for Raman and infrared spectra, respectively. The underlying data were obtained from ab initio molecular dynamics simulations carried out at 300 K for 32.5 ps on a bilayer structure in vacuum. The simulations were performed in CP2K³, where every eighth frame (4 fs) was selected to perform reruns for computing the volumetric electron densities required for computing infrared spectrum. For Raman, three more rerun simulations were performed with electric fields of magnitude 2.57 × 10⁹ V m⁻¹ applied along the X, Y and Z directions, respectively, to extract field-induced electron-density changes.

For infrared spectra, the dipole moment of the system was calculated at each frame by partitioning the electron density using the radical Voronoi tessellation method⁴. The molecular dipole moment μ_D is given by⁵

where Z_A and R_A denote the core charge and position of atom ‘A’ in a given molecule, and ρ(r) is the valence electron charge density partitioned to the molecule. The infrared absorption intensity is then obtained from the autocorrelation function of the time derivative of the dipole moment vector μ_D using⁶

where \(\widetilde{v}\) is the wavenumber, T = 300 K, \({{\varepsilon }}_{0}\) is the vacuum permittivity, c is the speed of light, N_A is Avogadro’s number, k_B is the Boltzmann constant, and \({ < > }_{{\tau }}\) denotes time averaging over τ. The derivatives of μ_D were evaluated using a second-order finite difference scheme.

The polarizability tensor, α, used for Raman spectra was computed from finite-field simulations⁷:

where μ_D,i is the ith component of the molecular dipole moment vector and E_j is the applied external electric-field in the jth direction. The isotropic and anisotropic (invariants) Raman scattering cross-sections were computed from derivatives of the polarizability tensor \(\dot{{\alpha }}\) using the expressions depicted in equations 4 and (5), respectively⁸:

Here, \({\widetilde{v}}_{\mathrm{in}}\left(\frac{1}{500}{\rm{n}}{{\rm{m}}}^{-1}\right)\) corresponds to the incident laser wavelength used for Raman scattering. All post-processing steps—including Voronoi tessellation, dipole moment and polarizability computation, autocorrelation function evaluation and spectral Fourier transforms—were carried out using TRAVIS^5,6,7,9.

To understand the origin of the various bands in the infrared and Raman spectra, we performed a generalized normal mode analysis as implemented in TRAVIS¹⁰. The objective of this analysis is to extract the normal mode frequencies and the corresponding atomic displacement patterns. Briefly, we computed the Fourier transform of the mass-weighted velocity cross-correlation functions to yield a frequency-dependent matrix, \(P(\widetilde{v})\), where¹⁰

Here, \({\Re }\) denotes the real part (corresponds to symmetrization over time forwards and backwards correlations), m_i and m_j are the masses of the ith and jth degrees of freedom, and \({\dot{x}}_{i}({\tau })\) and \({\dot{x}}_{j}({\tau })\) are the velocities of the ith and jth degrees of freedom. To decouple the vibrational modes, the integrals of the off-diagonal elements of \(P(\widetilde{v})\) are minimized using a modified Jacobi algorithm¹¹. This procedure determines an orthogonal transformation matrix, C, such that the transformed matrix \(\acute{P}(\widetilde{v})={CP}(\widetilde{v}){C}^{-1}\) has minimized off-diagonal elements. C is composed of new coordinate vectors—generalized coordinates—that define the normal modes of the system. The diagonal elements, \({\acute{P}}_{{ii}}(\widetilde{v})\), correspond to the power spectra of the decoupled normal modes. The frequency of each mode is determined by locating the maximum of its corresponding diagonal spectral component.

For the analysis, a monolayer trajectory was extracted from the bilayer ab initio molecular dynamics simulation, and translational motion was removed before post-processing. Once the normal mode frequencies were obtained, the modes corresponding to various infrared and Raman bands were identified and visualized using the MOLDEN¹² package.

We find generally good agreement between the bulk Raman spectrum and the simulated Raman spectrum. Amide I and II bands are assigned between roughly 1,450 cm⁻¹ and 1,650 cm⁻¹ to C–C aromatic stretching and C=O stretching of the amide groups^48,49. Amide III bands are assigned between roughly 1,220 cm⁻¹ and 1,280 cm⁻¹ as C–N stretching and N–H in-plane bending^48,49. Residual TFA is identified in both the bulk and 35-nm film samples at about 260 cm⁻¹ and 2,150 cm⁻¹ (ref. ⁵⁰) because of processing techniques. Although several of the amide bands are detected in the thin film, the signal is relatively weak over background photoluminescence because of the limited sample cross-section. However, a strong Raman band appears at 710 cm⁻¹ for the 35-nm film, which we attribute to symmetric stretching of the triazine cores^51,52,53. The total symmetric stretching vibration of triazine cores is typically observed between 680 cm⁻¹ and 690 cm⁻¹ but has been observed to shift to higher wavenumbers because of interaction with SERS substrates, along with notable signal enhancements due to preferential ordering at the SERS surface^52,53.

ATR-FTIR spectra (Supplementary Fig. 2b) were measured using a Bruker ATR-FTIR spectrometer with a reflection diamond ATR module. We again find good agreement between the bulk and simulated FTIR spectra. Amide I and II bands were assigned to C=O and N–H bending as well as C=O stretching of the amide groups between roughly 1,500 cm⁻¹ and 1,750 cm⁻¹ (Supplementary Table 1). Amide III bands are assigned to strong C–N stretching between roughly 1,110 cm⁻¹ and 1,350 cm⁻¹ (Supplementary Table 1). Strong N–H stretching observed around 3,500 cm⁻¹ in the simulated spectrum is found to be markedly broadened in the experimental data, a common occurrence due to intermolecular and intramolecular hydrogen bonding interactions that can weaken or shift the stretching frequency. The ATR-FTIR spectrum of the triple-stacked 35-nm film (about 100 nm total thickness) mirrors that of the bulk sample with the addition of signal from TFA (1,830 cm⁻¹, 2,100 cm⁻¹ and 2,300 cm⁻¹)⁵⁰. The most notable difference, however, is the relative suppression of the C–N stretching around 1,250 cm⁻¹ from the bulk sample to the thin film. The mechanistic reasoning for this change requires further investigation beyond this work, but our initial hypothesis is that this is due to the sensitivity of ATR-FTIR to molecular ordering through longitudinal vibrational modes⁵⁴.

Numerous non-crystalline and paracrystalline materials possess orientational ordering that is not captured by conventional X-ray techniques, including ordered polyaramid and cellulose fibres^55,56. Beyond XRD or direct imaging by electron microscopy, non-crystalline ordering can be detected using polarization-sensitive approaches⁵⁷. We demonstrate orientational ordering of a 35-nm 2DPA-1 film using polarized photoluminescence (Supplementary Fig. 4). We find that when excited at 532 nm with a polarized laser, the photoluminescence emission of the 35-nm 2DPA-1 film depends on its orientation with respect to the beam path. Specifically, the thin film emission transitions from roughly 1,400 cm⁻¹ (575 nm) when excited orthogonal to the beam path to 2,270 cm⁻¹ (605 nm) when excited parallel to the beam path. This twofold symmetry is consistent with anisotropic platelets oriented parallel to the substrate with a transition dipole along the long axis of the platelet⁸. We note that the emission window reported is beyond that of SiO₂ to eliminate signal interference.

Gas adsorption measurements

N₂ adsorption isotherms were measured at 77 K up to 100 kPa (1 P/P₀) using a low-pressure manometric instrument (Autosorb 6100, Anton Paar). The temperature was controlled using a liquid nitrogen bath. Before each isotherm measurement, the sample (about 0.220 g) was outgassed under high vacuum, with ramping rate of 1 K min⁻¹ from room temperature to 373 K and holding at that temperature for 12 h, before being cooled back down to room temperature and backfilled with N₂. The dry sample mass was determined after outgassing and before the isotherm measurement. The BET-specific surface area was calculated from a BET plot constructed in the classical BET range of 0.05 ≤ P/P₀ ≤ 0.3. The pore size distribution was determined using the Barrett, Joyner and Halenda method from the desorption branch (minus P/P₀ below 0.35) of the N₂ sorption isotherm at 77 K. The estimated 95% uncertainty was determined from two relative standard errors from measurements on two aliquots of the sample.

The N₂ adsorption isotherm of for 2DPA-1 platelets follows Type II isotherm behaviour (Supplementary Fig. 10a). It also possesses a type H3 hysteresis loop, which can be attributed to non-rigid aggregates of plate-like particles or pore network consisting of macropores that are not completely filled with condensate⁵⁸. The BET-specific surface area from the average of two aliquots is (74 ± 10) m² g⁻¹. The pore size distribution of powder 2DPA-1 consists of mostly mesopores, with an average mode pore width of about (11.1 ± 2.6) nm and some macro-porosity (Supplementary Fig. 10b). Bulk 2DPA-1 platelets have a total pore volume of (0.41 ± 0.07) cm³ g⁻¹. Given that the mode pore width is similar in size to the 2DPA-1 nanoplatelets (about 10–15 nm; Fig. 1b), this pseudo porosity is probably from interparticle space due to non-rigid aggregation of the 2DPA-1 platelets.

Unary He, H₂, CH₄ and CO₂ adsorption isotherms were measured at 298 K up to 1 MPa with a high-pressure manometric instrument (BELSORP-VC, Microtrac Bel). For measurements made in the high-pressure manometric system, the sample was outgassed ex situ in a tube furnace attached to a pumping station that is equipped with a turbomolecular pump (vacuum level of 10⁻⁷ Pa) backed by a scroll pump (vacuum level of 1 Pa). The following activation protocol was used: under high vacuum (0.1 Pa), the temperature was ramped up from room temperature to 373 K at a rate of 1 K min⁻¹, held at 373 K for 12 h and then cooled ( about 2 h) to room temperature to a final vacuum level of 10^–5 Pa. After activation, the sample was transferred under air- and moisture-free conditions from the sealed activator tube to an Ar glovebox for storage and transfer.

Inside the Ar glovebox, an aliquot (0.5391 g) of activated sample was loaded into the sample cell, which was then sealed, removed from the glovebox and connected to the instrument. The void volume was determined by means of helium expansion with 10 measurement points up to 3.5 MPa. The system contains one pressure transducer: 13.5 MPa with an accuracy of plus or minus 0.1% full scale. The temperature stability of the sample (plus or minus 0.1 K) was maintained by a water bath. The instrument air bath was maintained at (298 ± 0.1) K throughout the isotherm measurements. Before each isotherm measurement, the activated sample was reactivated at 373 K for 3 h to a vacuum level of 10⁻² Pa using a turbomolecular pump. Surface excess uptake was determined by keeping track of the moles of free gas in the system from the pressure and temperature readings and volumes of reference and sample chambers. The density of the gas was determined from the NIST Reference Fluid Thermodynamic and Transport Properties Database. The measurement uncertainty is 3 ml at standard temperature (273.15 K) and pressure (101.3 kPa) as reported by instrument manufacturer, which equates to 0.25 mmol g⁻¹.

The water vapour adsorption isotherm was measured using an automated dynamic vapour sorption analyser (VTI-SA⁺, TA Instruments) at ambient pressure with N₂ as the carrier gas. Bulk 2DPA-1 (about 15 mg) was outgassed for 12 h at 398 K under pure N₂ flow and then cooled down to 298 K. For the isotherm measurement, the relative humidity was determined with a dew point sensor and controlled by continuously mixing a dry N₂ (0% relative humidity) flow with a humid N₂ flow. The adsorbed amount is determined from sample mass changes during the vapour sorption experiment relative to the dry sample mass after outgassing. At each set relative humidity, equilibrium condition for the water uptake was set to sample mass change less than or equal to 0.001% in 99 min for a maximum time of 8 h. The instrument has a ±0.1 μg mass resolution and a relative humidity control standard uncertainty of plus or minus 1% based on manufacturer specifications. The adsorption of water on 2DPA-1 at low relative humidity implies an intrinsic hydrophilicity of the material (Supplementary Fig. 10d).

Preparation of 2DPA-1 thin films for bulge tests

We start by cleaning our Si/SiO₂ wafers with a 5-min sonication bath in acetone, followed by a 5-min sonication bath in IPA and finished by blow-drying with N₂. We then spin-coat a 10 wt% polystyrene in anisole solution onto the substrate at 2,000 rpm for 1 min and promptly transfer it to a hot plate at 110 °C, where it is annealed for 15 min to remove the anisole. We place a glass petri dish over the substrate during the annealing process to minimize the collection of debris on the polystyrene layer. We then spin-coat a solution of 2DPA-1 dissolved in TFA onto the polystyrene-coated substrate using the same spin settings. We can control the film thickness from roughly 60 nm down to 4 nm by adjusting the concentration of 2DPA-1 dissolved in TFA (Extended Data Fig. 1). The 2DPA-1 coated substrate is then quickly annealed on a hot plate at 50 °C for 5 min to evaporate any remaining TFA. We cut or trim away uneven areas of the film to ensure uniformity of the film thickness.

After our polystyrene-supported 2DPA-1 thin films have been prepared, we wet-transfer them to our etched substrates for bulge testing. To do so, we first clean the etched SiO₂ substrates using the same procedure for our SiO₂ wafers. We then use a razor blade to cut out the area of 2DPA-1/polystyrene film we would like to transfer from our wafer and bring the edge of this film to water so that it may lift the desired section of film off the wafer. With our section of 2DPA-1/polystyrene floating on the surface of the water (2DPA-1 facing the air), we quickly bring our etched substrate in contact with the 2DPA-1 side of the film and scoop it out of the water. The film-covered substrate is then left to dry overnight to remove any excess water. To form films that deflect downwards into the well, the substrates are annealed at 50 °C during the drying period.

After annealing, the films are placed in a glass petri dish with a 20-ml mixture of 25% v/v chloroform in hexane for 4 h to etch away the polystyrene support layer. We then transfer the substrates into a 20-ml mixture of 30% v/v chloroform in hexane as a polishing step for another 4 h. The substrates are then gently rinsed in hexane and air dried to remove any remaining solvents. 2DPA-1-coated substrates are stored at ambient conditions.

Relating change in bulge deflection to gas permeability

We account for the gas flux through the membrane with the ideal gas law:

where dn/dt is the change in the moles of gas inside the well over time, V is the volume of gas trapped under the 2DPA-1 film, R is the gas constant, T is temperature and dp/dt is the change in pressure over time. Because the volume contributed by the bulge’s deflection is much less than the volume of the 1-μm-deep etched wells, V approximates that of an etched well, πa²h/4. The permeability, \(\hat{P}\), of the film is thus related to the gas leak rate as follows

where Δp is the pressure difference across the film. The combination of equations 7 and (8) yields

We can relate the film deflection, δ, measured with AFM to the pressure difference between the microwell (p_int) and the external environment (p_ext) by

where the first term on the right side of equation 10 invokes Hencky’s solution⁵⁹ and the second term on the right side of equation 10 describes the influence of the initial surface tension of the film, S₀ (ref. ⁶). E and d are the film elastic modulus and thickness, respectively, the diameter of the microwell is represented as a, and K(ν) is a constant that depends on the film’s Poisson ratio, ν. We assign K(ν) = 3.09 for 2DPA-1, assuming it is equivalent to graphene in this case.

We solve the differential equation for p(t) and combine the result with equation 10, neglecting the initial-tension term, to obtain the relationship between the pressure differential and bulge deflection, δ, in logarithmic form:

where C is a constant of integration. Finally, rearranging and taking the derivative with respect to t yields the relationship between the film permeability and the rate of change for the bulge deflection:

Thermal degradation of bulk 2DPA-1 and temperature dependence of films

TGA-MS was carried out to analyse gas evolution at elevated temperatures during thermal degradation of 2DPA-1 (r = 10.5) in an inert N₂ atmosphere. The ramp rate was 10 °C min⁻¹ up to 1,000 °C. The off-gas was simultaneously analysed by a connected mass spectrometer. TGA-MS shows no trace of acetone (58 atomic mass units (AMU)), NMP (99 AMU), or pyridine (79 AMU) in low or high temperatures. This corroborates NMR results that show these chemicals are effectively removed during polymer purification³⁸. Water vapour (18 AMU) evolved from the 2DPA-1 sample between 65 °C and 90 °C probably corresponds to surface-bound (that is, physisorbed) water molecules. This is reflected in the first peak of the derivative thermogravimetric curve (Supplementary Fig. 12a). Water absorbed in highly confined pores requires substantially more energy to remove, often leading to desorption temperatures in excess of 100 °C (refs. ^60,61,62). Notably, we also detect water evolution from the 2DPA-1 sample between 300 °C and 450 °C. The release of water vapour observed at these elevated temperatures is beyond that expected from stronger confinement interactions and can instead be explained by the cleavage of the amide bonds during the thermal degradation of 2DPA-1. This is a well-studied mechanism in thermal degradation of similar polyaramids such as Kevlar and Nomex in which water is a common byproduct of thermal degradation^63,64.

As a hydrophilic material, water sorbed in the unit-cell pores of 2DPA-1 thin films may influence molecular transport of other gases. We investigated the potential effect of sorbed water on the gas impermeability of 2DPA-1 by means of a temperature-controlled environmental AFM stage (Asylum Research, Cypher ES Environmental AFM) to capture real-time measurements of four bulge deflections with respect to temperature (Supplementary Fig. 13a–d). All four bulge deflections decreased on the initial heating ramp up to 120 °C but did not result in complete deflation. We can thus conclude that pores blocked by water or residual TFA are not the root cause for the observed molecular impermeability of 2DPA-1, as the counter case would result in complete deflation on vaporization up to 120 °C. We attribute the decrease in deflection to a temporary and reversible opening of the rim seal, probably owing to the influence of heating on thermal expansion of the 2DPA-1 thin film and adhesion between 2DPA-1 and the SiO₂ substrate. When subsequently oscillating the temperature between 80 °C and 120 °C for 2.5 cycles, the bulge deflections similarly oscillated on the order of 10 nm.

Assuming no gas transport is occurring, we can predict the average change in the bulge deflection from 80 °C to a theoretical height at 120 °C through the series of equations shown below originating with the ideal gas law: \({P}_{1}{V}_{1}/{T}_{1}={P}_{2}{V}_{2}/{T}_{2}\). Here, the subscripts refer to states 1 and 2 of the bulge, and P, V and T are the internal pressure, volume under the bulge and temperature, respectively. By accounting for the geometry of the microwell system and using Hencky’s solution to relate bulge deflection, δ, to a pressure difference⁵⁹ (equation (10)), we can solve for δ₂ given T₁, T₂ and δ₁.

We set T₁ = 80, T₂ = 120 and δ₁ as the average experimental value at 80 °C in the oscillation regime (Supplementary Fig. 13e–h), with theoretical upper and lower bounds defined by the range of elastic moduli reported for 2DPA-1⁸. We find that 17 of the 20 (85%) experimentally determined deflections at 120 °C fall within the predicted range. Hence, our results do not indicate any discernible gas loss while oscillating between 80 °C and 120 °C and support the notion that physisorbed water is not the mechanistic explanation for the film’s measured impermeability.

Optical analysis of bulge deflections

AFM is the preferred technique to measure bulge deflection because of its high spatial resolution. However, AFM allows for limited control over environmental conditions as AFM tip calibration and tuning become distorted at non-atmospheric pressures and temperatures. We have therefore developed an optical technique that leverages the semitransparency of the polymer film to extract bulge deflections, allowing us to analyse the behaviour of bulges under non-atmospheric pressures and temperatures.

Light reflected from both the membrane and the bottom of the well undergoes constructive and destructive interference when collected at the detector, depending on the difference in optical path length. We exploit the resulting interference pattern to determine the degree of bulging (Extended Data Figs. 3–4). We illuminated our sample with a broadband light source (Thorlabs MCWHL5), where the reflected light passed through one of three optical bandpass filters (Semrock FBP01) with bandwidths of less than or equal to 16 nm and centre wavelengths (λ) of 440 nm, 540 nm and 600 nm, before being recorded by a camera (Extended Data Fig. 3a). We use MATLAB image processing tools to find the average intensities I(λ, r) as a function of the radial position, r (Extended Data Fig. 3b). A local maximum corresponds to a constructive (that is, bright) interference fringe, whereas a local minimum corresponds to a destructive (that is, dark) fringe. The static out-of-plane displacement δ(r) can theoretically be determined at any position from I(λ, r) if the intensities at destructive and constructive interferences, I_min(λ) and I_max(λ), are known⁶⁵. However, I_min(λ) and I_max(λ) cannot be easily extracted from local extrema because the amount of light that is reflected back along the optical axis depends on the local slope \({\rm{d}}\delta /{\rm{d}}r\) (Extended Data Fig. 3c).We therefore combine two different methodologies to determine δ(r) at all fringes as well as in the centre of the membrane, where \({\rm{d}}\delta /{\rm{d}}r=0\).

At each interference fringe with radius ρ, the deflection is a solution to

where the integer, q, is odd for minima and even for maxima. The optical path length difference for a flat membrane, ΔL, accounts for the gap, h, between the membrane and substrate, the phase shift of π at the substrate and the complex transmission and reflection coefficients of the membrane. To calculate the deflection in the centre of the membrane, we perform another calibration measurement. We measured the intensity, I(λ, r = 0), while incrementally decreasing the bulge deflection by manipulating the pressure inside the well. As long as the total change in optical path length exceeds one λ, we can define I_min(λ) and I_max(λ) as the lowest and highest measured values, respectively. Assuming that the centre point is aligned with the optical axis, the centre displacement is then a solution to

where q is an odd integer.

We identify solutions to equations 13 and (14) that match the parabolic deflection profile δ(r) that we expect based on theory and AFM measurements. To that end, we analyse the interference pattern for each wavelength as follows. Among the solutions to equation 13 for the outermost fringe, we select the value for q that corresponds to the smallest absolute deflection. Working towards the centre, we increase q by 1 for each subsequent fringe. At the centre, we assume that the deflection is within the range of \(\delta (r={\rho }^{* }) < \delta (r=0) < \delta (r={\rho }^{* })+\frac{\lambda }{4}\), where \({\rho }^{* }\) is the smallest observable fringe. The estimated bulge deflection is the average of the \(\delta (r=0)\) values obtained for each λ, with a standard deviation of roughly 10 nm. We extrapolate \(\delta (r)\) as shown in Extended Data Fig. 3d to confirm the validity of our calculations.

To make this technique more accessible to the broader scientific community, we apply it to an incoherent broadband light source that would be found on a common optical microscope. Here, we relate the bulge deflection to RGB pixel values from the optical image (Extended Data Fig. 5a,b). To physically connect the bulge deflection with its optical profile, we must first determine the combination of λ reflected by the sample into the camera using the Fresnel equations⁶⁶ and then convert those combinations detected by the camera into RGB pixel values.

The combination of reflected light wavelengths and their relative intensities when passing through three distinct layers (Extended Data Fig. 5c) can be calculated by⁶⁶

where r_j and \({\phi }_{j}\) are defined by the complex refractive indices (n) of layers j and j – 1:

The thickness of the layers is represented by d_j. Here, \({\phi }_{a}\) and \({\phi }_{b}\) are combinations of \({\phi }_{j}\) for the 2DPA-1 layer (layer 1) and layer of air trapped in the microwell (layer 2): \({\phi }_{a}={\phi }_{1}+{\phi }_{2}\) and \({\phi }_{b}={\phi }_{1}-{\phi }_{2}\). Layers 0 and 2 are air; hence, n₀ and n₂ are set to unity. The SiO₂ layer (layer 3) has a λ-dependent complex refractive index⁶⁷. We measured the refractive index of 2DPA-1, n₁, using a Filmetrics F20 reflectometer (Extended Data Fig. 5d).

Using equation 15, we plot I as a function of λ and film depth (that is, bulge deflection), represented here as the thickness of layer d₂ (Extended Data Fig. 5e). We then weighted I with the spectral power distribution of a 100 W tungsten halogen bulb and combined it with an assumed sensitivity of the detector to each λ. Because of the lack of information on the detector sensitivity, we assumed the sensitivity of the detector matches that of the human eye. This enables us to convert the combination of λ throughout the visible spectrum and their relative intensities to XYZ colour space and, finally, to RGB. In Extended Data Fig. 5f, we overlay the theoretical RGB values from this calculation with the measured data taken from Extended Data Fig. 5a,b after removing deflection data points between −100 nm and 15 nm, where a sharp discontinuity occurs because of edge adhesion effects and renders our three-layer model unsuitable. We find the model appropriately captures the relationship between RGB values and measured bulge deflection, albeit with a noticeable offset in the x and y directions. This offset stems from the assumed sensitivity of the detector as the human eye and could be improved on with more accurate information about the detector. We also note that the intensities of the measured R values seem to reach a saturation point, a likely result of the lighting conditions used throughout this study.

To perform our experiments in a controlled pressure and temperature environment, the sample is separated from the camera by another glass cover layer. This introduces two more layers to the model: the glass cover and another layer of air between the 2DPA-1 film and glass cover. This system thus requires a more complex formulation akin to equation 15, wherein there are 16 terms—rather than only 4—in both the numerator and denominator⁶⁶. Nonetheless, the overall form remains that of a linearly combined squared Fourier series and a discernible trend between the glass-covered RGB values and the AFM deflections remain evident.

To circumvent discrepancies between the existing theoretical model and measured data, we use a Fourier curve fitting function to produce practical relationships between the glass-covered RGB values and the bulge deflections measured in this study (Extended Data Fig. 6a). This enables us to extract valuable, dynamic information about the bulge deflections while they are in an environmental chamber. The sinusoidal relationship between R, G and B values are not one-to-one functions. Consequently, we cannot simply invert them to obtain a function of the form f(RGB) = δ. We instead obtain several deflection solutions for a single RGB triplet, necessitating the use of all three Fourier fit functions comparing the bulge deflection to independent R, G and B channels to minimize the number of solutions. Minimizing solutions aids in our ability to filter for the true deflection profile.

To eliminate extraneous solutions, we identify whether the local slope of a data point—when compared to its nearest neighbours—contributes to a bulge profile that is physically possible. Four quadrants are defined for physically possible bulge slopes. For a downwards deflected dimple, the slope is negative between the left-most edge and the centre (that is, pixels 0 to 50) and then positive between the centre and right-most edge (that is, pixels 50 to 100). For an upwards deflected bulge, the slope is positive between the left-most edge and the centre (that is, pixels 0 to 50) and then negative between the centre and right-most edge (that is, pixels 50 to 0). These physically expected slopes establish the constraints for viable solutions. Using a threshold of 35 nm to qualify two data points as neighbours, we keep only solutions that have at least one neighbour and obey the slope constraints expected for their quadrant. We display an example of solutions having passed this filter in Extended Data Fig. 6b.

We note that, even after filtering, remaining data can contribute to either negative or positive deflections. We thus introduce two more thresholds to determine the appropriate solution. The first threshold compares the number of data points contributing to either a positive (n₊) or negative (n_–) deflection, biasing the solution towards the larger dataset when n_+/− > 6.67n_−/+. If this condition is not met for either dataset, we introduce the second threshold. The second threshold compares the R² values of the positive \(({R}_{+}^{2})\) and negative \(({R}_{-}^{2})\) datasets, fit by a second-order polynomial in the form \(f(x)=a{x}^{2}+{bx}+c\), with f(x) = 0 at the bounds of the section profile. If \({R}_{-}^{2} > 0.7{R}_{+}^{2}\), then the negative dataset is selected and vice versa. These thresholds were manually determined by comparing the results for bulges with known negative and positive deflections. After selecting the negative or positive dataset, we perform two stepwise regressions to remove outliers from skewing the second-order polynomial fit. Data points that lie more than two standard errors away from the fit line are considered outliers and removed. The fit after these two stepwise regressions is the final prediction for the deflection profile based on the input RGB profile.

We extended this technique, which predicts the 2D deflection profile from a single diameter slice of an image, to predict the full three-dimensional deflection profile of a positively or negatively deflected film. We first isolated the image of the bulge from the substrate using standard image processing software and then created a mask to detect the edges of the bulge and calculate its centre and diameter. Next, we used polar coordinates to discretize the bulge into 1° increments, obtaining 180 radial diameter slices of the bulge at different degrees about its centre. These radial slices can be individually analysed with the parabolic fitting method, then reconstructed to yield a three-dimensional height profile of a bulge (Extended Data Fig. 6c,d). We note that each slice is not in complete agreement about the direction in which the bulge is deflected. To obtain agreement, we first identify the direction of the deflection (that is, positive or negative) based on the majority response of the 180 slices. We then fit a single second-order polynomial to all the relevant slices and perform two stepwise regressions, where outliers are again defined as more than two standard errors away from the fit. The final fit obtained from this processing is used to define the cross-sectional profile of the three-dimensional bulge and construct a three-dimensional deflection profile.

Resonance measurements

We measured the thermal displacement fluctuations of the fundamental resonance mode with a path-stabilized homodyne Michelson interferometer as shown in Extended Data Fig. 4. We used a stabilized HeNe laser with λ = 633 nm and a peak power of 3 mW. The spot size (full width at half maximum) on the sample is about 800 nm, and the incident power is about 600 µW. Two photodetectors are used in this setup, PD₁ (New Focus 1801) for displacement measurements and PD₂ (Thorlabs PDA8A) for path stabilization. After taking a measurement at the antinode (that is, the centre of the suspended film), we take a second measurement with the same parameters on the polymer film adjacent to the well to determine the background noise level in our measurements, such as low-frequency laser noise or cable resonances. For both measurements, we averaged 10³ data traces. Based on the assumption that different noise sources are uncorrelated, we subtracted our background noise from the noise measured on the suspended film.

DFT and molecular dynamics simulations

DFT calculations were performed on bilayer configurations with various interlayer offsets to determine the most stable configurations (minimum energy). The interlayer offsets were generated on a 4 × 4 grid in the x–y plane with a maximum shift of 8.3475 Å along each axis. For each offset, the system was first relaxed by performing a geometric optimization in vacuum using DFT. The interlayer interaction energy, E_int, for the final optimized geometry was computed as

where E_bl is the energy of the bilayer and E_ml–1 and E_ml–2 are the energies of the two monolayers.

To investigate the interaction of various gases with the 2DPA-1 membrane, a 3 × 2 × 1 supercell was constructed from the experimentally obtained crystal structure of a 2DPA-1 unit cell. This supercell was geometrically optimized with DFT, and a bilayer structure composed of two such layers stacked together was generated. Various configurations were generated by offsetting the adjacent layers relative to each other along the x axis (Supplementary Fig. 17).

To determine the translocation energy profiles for CO₂, N₂ and Ar, a single gas molecule was positioned at the centre of a pore in the bilayer membrane at varying distances along the z axis (translocation axis) from the membrane (Supplementary Fig. 17). The membrane-gas interaction energy, E_int, was computed as

where E_m+g is the energy of the combined membrane and gas system, E_m is the energy of the membrane alone, and E_g is the energy of the isolated gas molecule. These energies were calculated using DFT, as implemented in the CP2K package⁶⁸. Single-point energy calculations were performed with the Gaussian and Plane Wave scheme⁶⁹, using a plane-wave cutoff of 500 Ry. The Geodecker–Teter–Hutter pseudopotentials⁷⁰ and triple-zeta valence polarized basis sets with molecularly optimized functions⁷¹ were used for all atoms. The Perdew–Burke–Ernzerhof exchange-correlation functional⁷², combined with D3 dispersion correction⁷³, was used for these calculations.

To ensure physical validity, initial structures were energy minimized with pore atoms allowed to relax while keeping the gas molecules fixed. Because of the computational cost of DFT, energy minimizations were performed using the Optimized Potentials for Liquid Simulations classical interatomic potential in GROMACS^74,75,76. The force-field parameters for 2DPA-1 were derived using the LIGPARGEN tool^77,78,79 and BOSS⁸⁰ implemented by POLYPARGEN⁸¹, and the parameters for CO₂, N₂ and Ar were sourced from previous studies^82,83.

Energy profiles were plotted along a uniform grid with a spacing of 0.5 Å along the translocation axis. For each gas and membrane offset, the energy barriers, E_barrier, were determined as

where E_max and E_min are the maximum and minimum interaction energies along the z axis, respectively. The resultant barrier versus offset plots for CO₂, N₂ and Ar are shown in Supplementary Figs. 18 and 19.

To identify the interlayer offset that results in the maximum gas translocation energy barrier, we conducted further DFT energy calculations using the same protocols outlined above. In this series of calculations, gas molecules were held fixed at three distinct positions along the translocation axis (Extended Data Fig. 8a) while the pore-to-pore offset between the membrane layers was varied from 0% to 72%. For each offset, the interaction energy between the membrane and the gas molecule was computed using equation 19. Introducing offsets between the layers results in the splitting of the pores into two separate regions. Consequently, for each offset and gas position along the translocation axis, we considered two distinct configurations by positioning the gas molecule in each of the two resulting pores. The barrier for a given offset was determined as the minimum of the two interaction energies (Extended Data Fig. 8b).

We accounted for entropic effects on the free energy barrier during gas translocation across the 2DPA-1 bilayer by computing the potential of mean force (PMF). We focused on the most sterically restricted case—a 60% pore-to-pore offset (Supplementary Fig. 20). We note that the energy barriers determined from the PMF profiles should be interpreted more qualitatively than quantitatively. The PMF profiles for CO₂, N₂ and Ar were obtained using the umbrella sampling technique⁸⁴. In this approach, gas molecules were constrained at various positions along the translocation axis relative to the membrane, with each position representing an umbrella window. A harmonic potential with a force constant of k = 50,00 kJ mol⁻¹ nm⁻² was applied to constrain the gas molecules in all three spatial directions. Each simulation window was run for 10 ns at 300 K using the Optimized Potentials for Liquid Simulations force field to ensure adequate sampling. Histograms of the gas molecule positions were generated from the simulation data, and the PMF profiles were computed using the Weighted Histogram Analysis Method⁸⁵, as implemented in GROMACS with the g_wham tool⁸⁶.

Monte Carlo simulations

Frameworks of stacked 2DPA-1 platelets were generated layer by layer, where the 2DPA-1 platelet is represented by an array of pores with a radius of 5 Å (r_p) and centre-to-centre spacing of 2.42 Å. Each adjacent layer is separated by a predefined pore offset between 0% and 100% (that is, 0 to 2r_p). The offset angle between adjacent layers is randomized between 0 and 2π for each additional layer. The transport area under consideration is 8 nm × 12 nm with periodic boundary conditions to approximate an infinite planar system without defects.

We probe the transport of gas molecules across the 2DPA-1 lamellar framework using an effusion-based hit-and-miss methodology³⁰. This simplified approach treats gas molecules as hard spheres with a radius defined by their kinetic diameter. Impingement attempts by the gas molecules result in successful permeation events if they pass through an effective pore in the 2DPA-1 lamellae without interacting with the pore edge. In other words, gas molecules that contact any part of the impervious 2DPA-1 framework are considered sterically excluded. An effective pore in this case is considered vertically continuous free volume across the 2DPA-1 lamellae formed by the overlapping of in-plane pores by adjacent 2DPA-1 platelets. We probe the framework with 10⁴ gas molecules of random location to determine the percentage of successful permeation events. This number was chosen based on a sensitivity analysis to minimize computational cost without significant loss of accuracy (Supplementary Fig. 15). Results from the Monte Carlo simulations were compared against analytical solutions in Supplementary Fig. 16. Deviation between the two results above an offset of 60% stems from the difference in offset angles. For the analytical solution, the offset angle is taken as 0, whereas the Monte Carlo framework is randomized.

Confined diffusion

A confined diffusion is characterized by a MSD of the form^87,88,89

where R_C is the characteristic size of the region of confinement, D is the diffusion coefficient, t is time, and A₁ and A₂ are geometric constants. We fit equation 21 to the longitudinal data found in Fig. 3 and Supplementary Figs. 22 and 23 to extract the R_C for each dataset.

Fabrication and characterization of 2DPA-1-coated perovskites

Three-dimensional MAPbI₃ perovskite was prepared in a two-step process: Si substrates were first cleaned with UV-Ozone (Jelight Company Inc.) for 20 min. In parallel, PbI₂ beads were added into a 9:1 solvent mixture of dimethyl formamide:DMSO with a concentration of 2 mmol l⁻¹. Meanwhile, methylammonium iodide (MAI) powder was added into isopropanol with a concentration of 1 mmol l⁻¹. Then, 30 µl of PbI₂ was spin-coated onto the cleaned Si substrate at 2,000 rpm for 1 min. The substrate was subsequently annealed at 70 °C for 1 min. The MAI solution was then spin-coated onto the PbI₂-coated substrate at 2,000 rpm for 1 min. The substrate was then annealed at 150 °C for 10 min to form a three-dimensional MAPbI₃ thin film. A 10 mg ml⁻¹ solution (in TFA) was spin-coated onto the MAPbI₃ surface at 2,000 rpm for 1 min. The resulting composite were annealed at 100 °C for 5 min to remove any residual TFA. 2DPA-1-coated perovskite films were characterized using XRD with a Rigaku Smart Lab, using a Cu Kα source (λ = 1.54056 Å) in Bragg Brentano mode.

Relating bulge lifetime to 2DPA-1 permeability

To elucidate the inhibition of molecular transport across the 2DPA-1 thin film, we consider three viable transport pathways: (1) through the 2DPA-1 unit-cell pores, (2) through a Knudsen pore formed by interconnected voids in the film, or (3) through both the unit-cell pores and non-connected voids in the film (Supplementary Fig. 11). We assume no interlayer transport because of the absence of free volume between stacked platelets. For the second pathway, gas permeability across the film \((\hat{P})\) can be modelled using classical effusion³⁰:

where \(\hat{P}\) depends on the film porosity (σ), gas molecular weight (M_w), ideal gas constant (R) and temperature (T). \({\hat{P}}_{{{\rm{N}}}_{2}}=7\times {10}^{-2}\) Barrer is predicted by equation 22 for a 35-nm-thick film suspended across the Si/SiO₂ microwell in the limiting case of only a single 1-nm-diameter Knudsen pore. A permeability this high would lead to a 99% loss of overpressure (that is, pressure above atmospheric) in only a few seconds for a bulge of any thickness (Supplementary Fig. 11). We refer to this threshold for the overpressure loss as the bulge lifetime (t), which can be determined by treating the gas efflux from the sealed microwell as a first-order decay process:

where τ is the time constant for the decay rate and l is the depth of the microwell. The short lifetime of bulges possessing any Knudsen pores, which would not survive long enough to be measured in AFM, disqualifies effusion-based mechanisms. We therefore postulate that gas transport, if occurring at all, must take place by means of passage through the 2DPA-1 unit-cell pore.

This approach can also be leveraged to determine the maximum permeability threshold for bulges that do not deflate over the observation period (t_obs). If no significant loss of overpressure occurs, evidenced by a lack of negative change in the bulge deflection, we can safely assert that the bulge did not reach the half-life (t_1/2) of its deflation over the duration of observation, where \({\rm{\Delta }}p(t)={\rm{\Delta }}{p}_{0}/2\). The maximum allowable permeability necessary for a bulge to maintain half of its overpressure (that is, stay inflated) over that observation period can be extracted from equation 23 by assigning t_1/2 as t_obs.

Positively deflected bulges that formed from the trapping of excess air molecules between the 2DPA-1 film (35-nm to 4-nm films) and Si/SiO₂ substrate during film transfer remained inflated for days, with some persisting up to the longest measurement period of 2 months (Extended Data Fig. 1). Using equation 12, we can relate the change in bulge deflection over time to the flux of air out of the sealed microwell. We find the deflection rates of the 2DPA-1 bulges span several orders of magnitude and lack a thickness dependence, illustrated by deviance from intrinsic permeability curves (Extended Data Fig. 1), that would otherwise demonstrate transport occurs solely across the accessible film area. This finding is akin to previous measurements of gas transport across graphene suspended on Si/SiO₂ substrates⁶ and implies that gas leakage is occurring variably through the seal between the 2DPA-1 film and microwell interface. We term this interface the rim seal.

Importance of the rim seal in forming persistent bulges

Eliminating interfacial leakage is essential to measure the intrinsic permeability of a suspended film; hence, various efforts such as ultrahigh pressure sealing with a diamond AFM tip²⁴ and the fabrication of graphitic microwells^5,34,90 have been pursued to improve the rim seal for suspended graphene. The effects of eliminating interfacial leakage can be substantial. By suspending graphene monolayers on graphitic rather than Si/SiO₂ microwells, gas efflux was eliminated entirely. To control the internal gas environment of a persistent bulge without interfacial leakage, the following must occur: the interfacial rim seal must open on external gas exposure, sufficient time must be given for pressure equilibration on both sides of the film, and the rim seal must close after removing the external gas.

Non-deflected films suspended over microwells often indicate a poorly sealed interface, leading to the quick deflation of bulges formed after pressurizing. By contrast, the existence of negatively deflected films (that is, downwards dimples) necessitates an adequate rim seal to prevent atmospheric air from equilibrating the negatively pressurized microwell. We therefore put emphasis on starting with downwards dimples to minimize effects from defective rim seals and maximize the success rate of pressurizing bulges with desired gases.

The ideal gas law dictates that ambient gas trapped in the microwell at an elevated temperature when the rim seal is formed will have a lower pressure than the atmosphere on cooling. We targeted the formation of negatively deflected films by annealing our sample overnight at 50 °C immediately after transferring the film to the Si/SiO₂ substrate. Pressurizing negatively deflected films led to a near-perfect rate of forming persistent bulges when using N₂.

Solution-phase properties that give rise to impermeable films

To gain deeper insight into the r-dependent size variations among 2DPA-1 samples, we used fluorescence measurements of 2DPA-1 in TFA (Supplementary Fig. 27). Solution-phase fluorescence measurements were measured with Duetta fluorescence and absorbance spectrometer from Horiba Canada Inc. To prepare the samples, we suspended the 2DPA-1 powders into TFA at a concentration of 1 mg ml⁻¹ and then sonicated in a Branson ultrasonic cleaner for 15 min. The solution was then added into a quartz cuvette for measurement.

The 2DPA-1 with r = 2.27 shows three main features, with a predominant excitation feature around 350 nm that is not present in the r = 9.67 sample. The large associated Stokes shift (greater than 100 nm) for this feature compared to the smaller Stokes shift (less than 50 nm) observed around an excitation of 450 nm indicates that the lower-r sample possesses a greater abundance of small particles in solution—a phenomenon that is well-established for various nanomaterials^91,92,93,94. We find a strong dependence on the ability of the 2DPA-1 films to suspend over the microwells with their associated platelet r parameter (Extended Data Fig. 9). This analysis was conducted by quantifying the yield of suspended films using optical microscopy (Supplementary Fig. 28). Below an r value of 4, all films collapsed into the microwell, whereas the yield for films with higher r values approach 100%. Previous work has alluded to the importance of interlayer interactions in the mechanical integrity of thin films made from 2D materials⁹⁵. We therefore posit that the films made from 2DPA-1 with a high r parameter benefit from increased mechanical integrity due to an abundance of interlayer interactions between large areas of overlapping platelets.

Calculation of 2DPA-1 density

We derived the theoretical density of 2DPA-1 using a combination of experimental data and literature sources. We begin with the following expression:

where \({\rho }_{{\rm{A}}}\) is the areal density of a single 2D platelet, and m_p, A_p and d_p are the molecular mass, area and thickness of a platelet, respectively. For this calculation, we analysed an infinite hexagonal platelet and treated it as a hexagonal cylinder. We normalized m_p and A_p to be per monomer. In an infinite platelet, m_p corresponds to two monomer types (Supplementary Fig. 26a,b). We thus averaged the molecular mass of both monomers, yielding 141.1 g mol⁻¹ for m_p.

We then determined the area of the unit-cell six-membered ring, A₆ (Supplementary Fig. 26c), to calculate A_m. Each monomer is part of three six-membered rings; therefore, one third of each monomer’s area is in the single-unit-cell ring. Given the six monomers per ring, A_m = A₆/2. We used literature values of melamine, terephthaloyl chloride, a bifunctional proxy for trimesoyl chloride and amide peptides (Supplementary Table 2 and Supplementary Fig. 26d) for the bond lengths and angles of the six-monomer ring of 2DPA-1. Consequently, we obtain a side length of 6.562 Å for the unit-cell ring and A_m = 55.93 Å as a result. Pairing these calculations with previous measurements of d_p (ref. ⁸) gives us a volumetric platelet density, \({\rho }_{{\rm{V}}}\), of 1.14 ± 0.09 g cm⁻³.

Platelet defectiveness

A perfect hexagonal platelet has unreacted groups only along the periphery of the platelet, whereas a defective platelet with branches or missing interior monomers would have unreacted groups along the periphery and along the defects. It was previously found that 2DPA-1 platelets have 0.28 acyl-group nm⁻² in excess of a perfect platelet with the same corresponding diameter⁸. Thus, we find it necessary to consider this amount of defectiveness in our comparisons.

We define the defectiveness of a platelet by comparing how close a platelet is to the perfect hexagonal case using

where D is the defectiveness, U is the number of unreacted sites on the platelet, and M is the number of monomers that the platelet consists of. This differs from a ratio of r values as r only accounts for the trimesoyl chloride monomer. When calculating the defectiveness, we use the M_perf/U_perf ratio of the perfect platelet with corresponding total diameter. For a fourth-generation perfect platelet, M_perf/U_perf = 3.

Analysis of O₂/H₂O permeability in 2DPA-1 thin films by means of perovskite degradation kinetics

The degradation of MAPbI₃ perovskites has been intensively studied, and it is generally accepted that ambient oxygen (O₂) and water (H₂O) play essential roles in the degradation process^96,97,98,99. XRD is the most common technique to monitor MAPbI₃ film degradation because the (110) peak of MAPbI₃ at 2θ = 14.1° and signature (001) peak of the degradation product PbI2 at 2θ = 12.7° can be easily discerned and tracked. More importantly, given that the sample is fixed in position, the two diffraction patterns are fully comparable in both shape and intensity⁹⁶. The colorimetric changes of MAPbI₃ films in ambient conditions can be another sign of degradation¹⁰⁰. Specifically, freshly made MAPbI₃ films exhibit a dark black colour (that is, black phase), whereas degraded MAPbI₃ films containing mostly PbI₂ and MAI exhibit a yellow colour (that is, yellow phase). The precise role of O₂ versus H₂O in MAPbI₃ perovskite degradation remains unclear, and many different design strategies and barrier materials have been explored to slow down the degradation¹⁰¹. When designing barrier materials for three-dimensional perovskite optoelectronic devices, it is optimal to have the materials that serve both as encapsulation layers and as electron or hole conduction layers, and this property is not explored in this work.

We analysed the time-dependent XRD data from Fig. 4g,h to extract the kinetics of solid-state reaction with ambient O₂ and H₂O, both with and without 2DPA-1 barrier protection. By comparing the relative rates of PBI₂ formation from these reactants for these two perovskite systems (protected and unprotected), we can estimate the permeability of these two reactants. The chemical kinetic and mass transfer model for this system are derived below. The 650-nm perovskite film was left exposed to ambient humidity (25% relative humidity) and temperature (298 K) with or without a protective 60-nm 2DPA-1 coating. XRD spectra were collected at varied time intervals along with images documenting the colorimetric change, consistent with the rate of degradation.

Our simplified kinetic model considers the degradation of Phase A (MAPbI₃) to Phase B (PbI₂) driven by the ambient reactant gas driving the gas (labelled G):

The overall kinetics are modelled using the second-order reaction rate: \({r}_{{\rm{A}}\to {\rm{B}}}={k}_{{\rm{in}}}{C}_{{\rm{A}}}{C}_{{\rm{G}}}\), where k_in is the intrinsic rate constant, C_A is the concentration of Phase A, and C_G is the concentration of the reactant gas. The cases of unprotected and protected perovskite systems reduce to first-order reactions. For the unprotected system, the reactant G is necessarily in excess. The reaction of Phase A to Phase B thus reduces to

where the reaction rate is defined as \({r}_{{\rm{A}}\to {\rm{B}}}=k{C}_{{\rm{A}}}\), with k = k_inC_G. For the protected system, the concentration of reactant G at the perovskite surface is reduced significantly but assumed to be kept at a reduced steady state such that the first-order reaction above applies to this case.

The coordinate system for the 2DPA-1-coated perovskite is depicted in Extended Data Fig. 10. Diffusion of reactant G into the perovskite lattice is considered fast compared to all other rates in the system such that its concentration is considered uniform throughout the perovskite lattice. In other words, the concentration of reactant G throughout the perovskite lattice is equivalent to the concentration at the perovskite surface, C_Gδ. The decay of Phase A to Phase B is first order with rate constant k = k_inC_Gδ. For the unprotected perovskite, the ambient concentration of the reactant G, C_G0, is equivalent to C_Gδ. For Phases A and B with starting compositions in the perovskite lattice of C_A0 and C_B0, respectively, the kinetics of the conversion are

The ratio of the XRD peak areas for Phases B and A, P_A/P_B, is proportional to the composition ratio C_B(t)/C_A(t) through constant α assumed as unity for C_B0/C_A0, the initial ratio at t = 0 (P_A0/P_B0). The kinetics of the ratio should thus be described by

and, hence, a plot of peak ratios versus time should be linear with zero intercept and a slope equal to k, the pseudo-first-order rate constant of perovskite decay (Extended Data Fig. 10b).

For the case of the 2DPA-1-coated perovskite, we treat the transport of reactant G in the polymer layer as classic Fickian diffusion:

The boundary conditions are C_G = C_G0 at x = 0 and C_G = C_Gδ at x = δ. The concentration profile of reactant G in the 2DPA-1 film is linear

and the diffusive flux at the perovskite interface (x = δ) must equal the rate of the reaction for G in the well-mixed perovskite lattice; hence

The concentration of reactant G at the perovskite interface (x = δ) is then

where ϕ is the Thiele modulus—or ratio of reaction to diffusion rate—applicable for this system. The analysis of the perovskite lattice above applies with the pseudo-first-order rate constant modified by ϕ:

We display the analogous plot of the XRD peaks for the case of the 2DPA-1-protected perovskite in Extended Data Fig. 10b. The linear dependence yields a first-order reaction rate constant of 7 × 10⁻⁷s⁻¹. The square of the Thiele modulus, \({\phi }^{2}\), is found from the rate constant ratio of the unprotected and protected cases: \({\phi }^{2}={k}_{{\rm{uncoated}}}/\)\({k}_{{\rm{coated}}}-1\) = 14.3. The diffusivity of G in 2DPA-1 thus found to be 2.93 × 10⁻²⁰ m² s⁻¹. In standard permeability units (D_G/RT) at 298 K, the value is 1.1 × 10⁻²³mol m⁻¹ Pa⁻¹ s⁻¹ or 3.3 × 10⁻⁸ Barrer.