How would you go about answering the question “How many people have ever lived on this planet?” If you type that into Google or an artificial intelligence chatbot, you’ll get an answer pretty quickly—usually 117 billion. That number, at least in my opinion, seems far too small. After all, the world’s population is currently estimated at 8.2 billion people. That means we make up about 7 percent of all people ever born.
The 117-billion figure includes every person who has ever seen the light of day—including those who died young. Life expectancy has increased globally over time, however. As a result, there are other strange population questions to consider. For example, a 2014 article in the Economist stated that half of all people who have ever been age 65 or older are alive today. Can that really be true? And how do you even calculate something like that?
Demographers have been asking such questions for decades. One of the biggest challenges they face is from the data: you need to know how many people have lived at different times, as well as the average life expectancy or birth rate. Such numbers are available today (though records are not always reliable) but less so for centuries past. Statistical analyses and censuses have not been routinely carried out everywhere and across all societies. Demographers must therefore rely heavily on estimates.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
And then there are a few fundamental questions to consider. What exactly is meant by “human”? Do we mean all members of the genus Homo who have walked our planet or just Homo sapiens in particular? Given the challenges, it’s astonishing that when estimating all the people who have ever lived, we are usually only presented with one number, 117 billion, rather than a range with a low and a high estimate. I argue that that is entirely appropriate from a scientific point of view and signals that the result is an approximation. The order of magnitude may seem plausible, but the question cannot be answered exactly.
Modeling Population Growth
To realistically assess the 117-billion-person estimate, you first need data. From the 20th century to the present, you can find lots of population figures, thanks to regular censuses conducted in many countries since the 1850s.
Looking further back in history, the number of people living can be roughly estimated based on the size of cities and population density. For even earlier times, archaeological remains offer clues.
Nevertheless, some sources put the world population in the year C.E. 1 at 170 million people and others at 300 million, almost double that number. There is also the question of how far back we should even look. There are estimates in which demographers go back as far as 4.5 million years to consider all members of the genus Homo. Others, however, focus on Homo sapiens and look back between 50,000 and 200,000 years.
Over the years, not only the number of living humans but also the corresponding rate of population growth has changed significantly. The world’s population used to increase very slowly but seems to have grown faster in recent centuries. That’s because the birth rate has decreased while the death rate has decreased even more—a combination that can be difficult to model.
The growth rate can be assumed to be constant for small time intervals, however. Demographers use that assumption to estimate the number of all living people in a given time interval. You have to divide the period under consideration into different sections; for example, you can start 50,000 years before our era and end in the year 2025. The more subdivisions you make, the more accurate the result.
If we now assume that the birth rate g and death rate s are constant within a section of that timeline, then the population size N changes according to the following differential equation:
Given that g and s are assumed to be constant within an interval, the population size in this area can be modeled using an exponential function: N(t) = N0ekt, where the parameters k (the net growth rate) and N0 (the population size when time t = 0) are determined by the data points.
To determine how many people have ever lived, you have to add up the number of all living people at each point in time t. This can be done by calculating the integral of the piecewise-defined function over t in the respective section:

This approach overestimates the actual answer, though. Think of it this way: If you are reading this article, then you are currently alive; you were most likely already alive 10 years ago, however, and also contributed to the world population back then. The integrated result must therefore be divided by the respective life expectancy of the people who lived during the period in question. At the end, you can add up the results for all time periods and—ta-da!—the result should correspond to the total number of people who have ever lived.
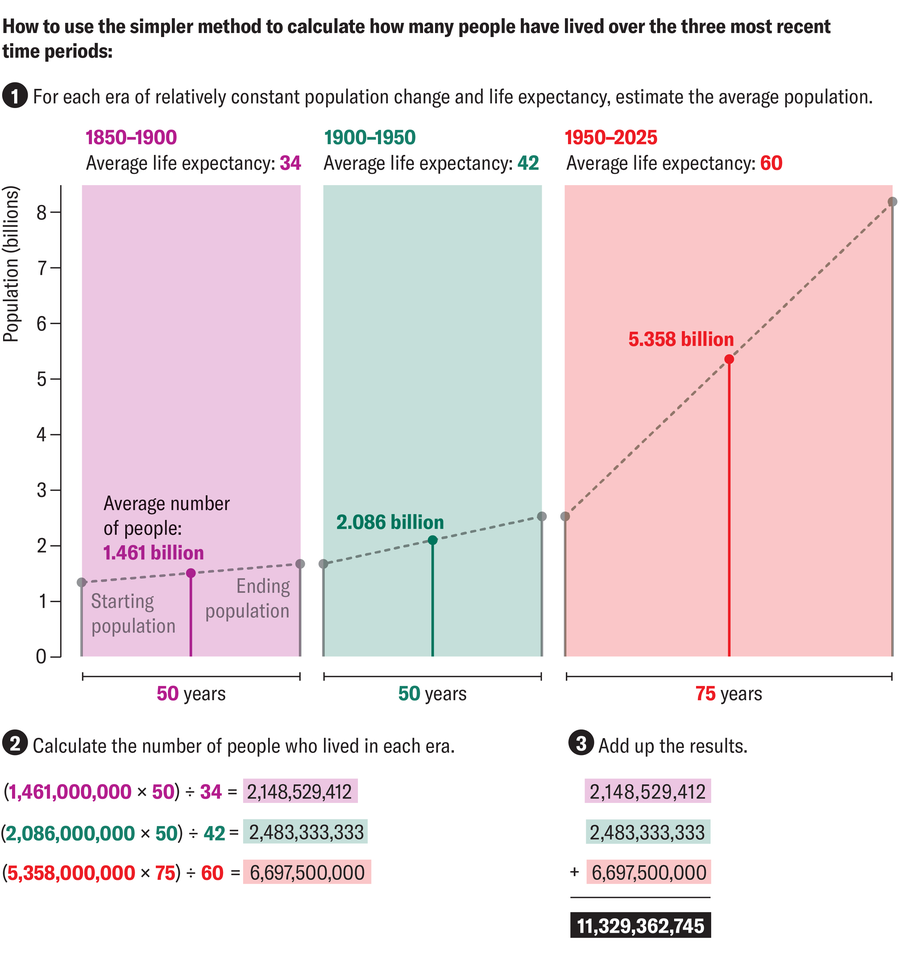
Technically, there is a simpler approach, as German math teacher Bruno Scheja demonstrated with a school project. He set his pupils the same task: they were to estimate the number of all people who have ever lived. But these students did not yet know how to calculate the integral of an exponential function.
One group of students decided to simply calculate the mean value for specific time intervals. For example, if there were around 1.6 billion people in 1900 and 2.5 billion in 1945, the students assumed that an average of 2.05 billion people lived within these 45 years. They then multiplied these average values by the respective time period (45 years, in this case) and divided them by the average life expectancy that people had at that time (by taking an average of the lifespans in 1900 and 1945). This method gave the group a rough estimate of the entire world population without having to resort to complicated calculation methods such as integrals.
Two Methods with Surprisingly Similar Results
To compare these techniques, you can calculate the population figure using an example. I have opted to use data that were previously used by demographer Carl Haub in a Population Reference Bureau article published in 2011. He assumed that humanity originated 50,000 years ago with two people. He also estimated life expectancy for each time interval.
I have added a final data point with the estimated population and life expectancy in 2025.
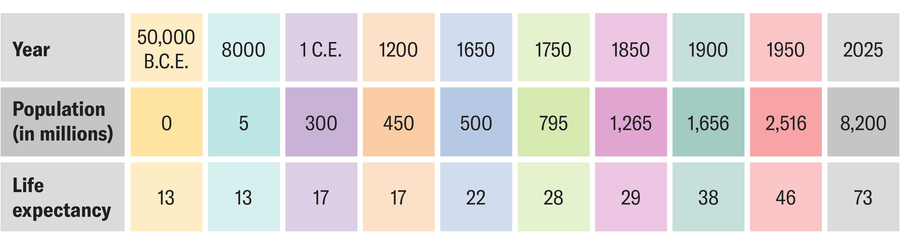
In total, there are 10 points available in this example that delimit nine sections. Within these, suitable exponential functions can be defined to model the respective growth. By dividing these by the average life expectancy in this period, you can obtain the number of people alive at that time.
This leads to the conclusion that slightly more than 93 billion people have ever been born. The 117-billion figure is based on a more recent estimate from Haub and demographer Toshiko Kaneda that appeared in 2022 with updated population data. (The researchers assumed, among other things, that the human race originated 200,000 years ago.)
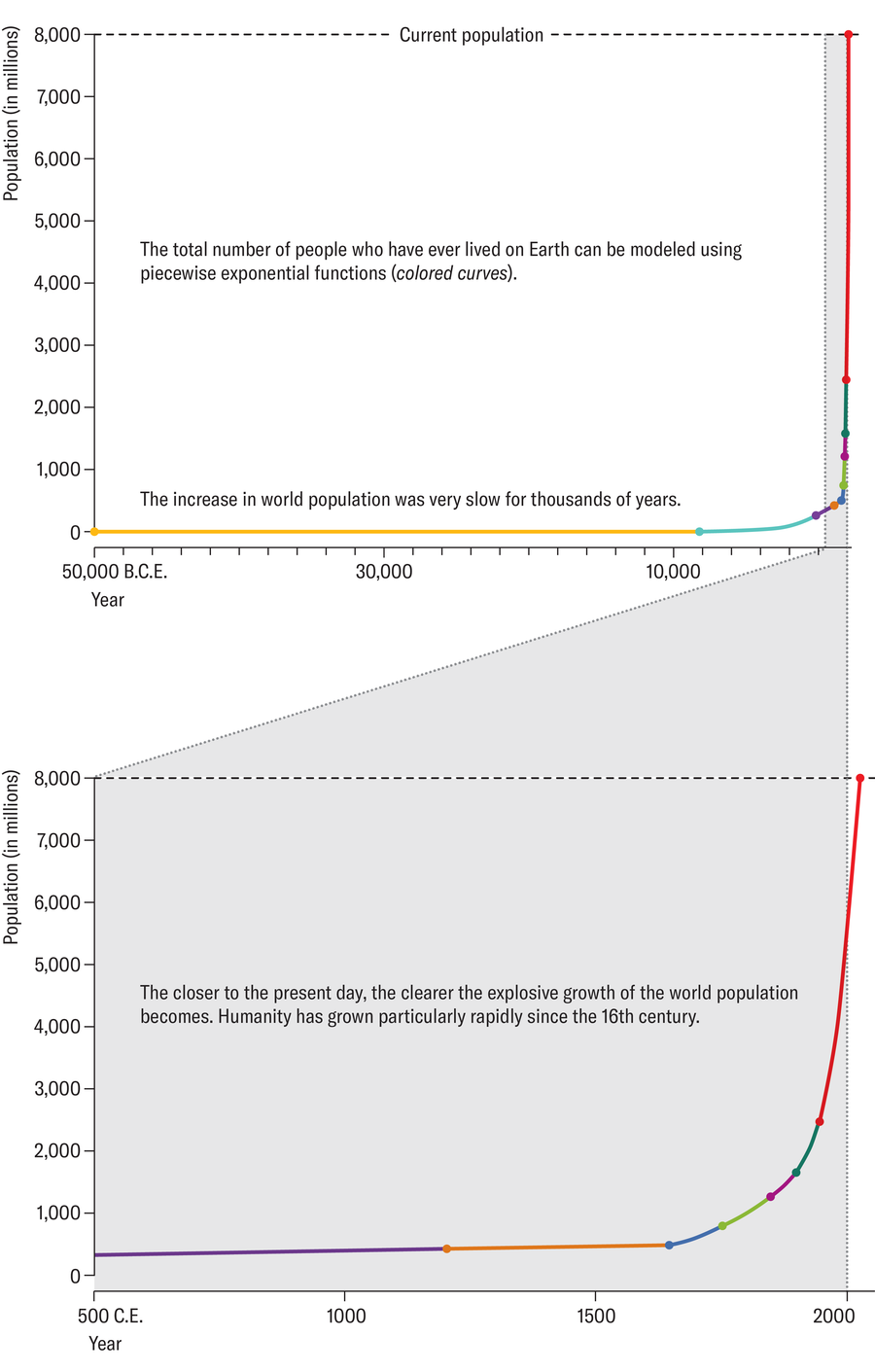
If you apply the simpler calculation method used by Scheja’s students to the data from the above table, the final result is more than 140 billion—significantly more than the result obtained by the other method. This difference may seem large, but it is actually impressive that it ends up being the same order of magnitude.
What about People Age 65 and Older?
The two approaches presented make it possible to estimate how many people have ever been born. But what about the statement by journalist Fred Pearce in his 2010 book The Coming Population Crash that of all people who have ever reached age 65, half of them are alive today? In 2017 a team of demographers led by Miguel Sánchez-Romero of the Wittgenstein Center for Demography and Global Human Capital examined this statement after it resurfaced in a 2014 Economist article. The researchers developed two different demographic models to investigate: one in which population growth was constant and a second in which they considered hyperbolic population growth.
They also used various datasets for their modeling to provide realistic error estimates. Their conclusion: Fred Pearce was incorrect. “Indeed, such a number would be never attainable, neither theoretically (in a stable population), nor empirically according to existing data,” they wrote in their paper.
According to their calculations, the proportion of people who have ever reached age 65 or older who are alive today is between 5.5 and 9.5 percent. This means that even in the most extreme case, just under 10 percent of all people who have ever been age 65 or older are alive today. Even if this significantly softens Pearce’s original statement, I still find the result quite astonishing. Imagine there were a kind of lottery that decided at what point in human history you would be alive based on your lifespan. If you reached the age of 65, you would have a probability of around one in 10 of being alive today—even if you take into account the past 200,000 years.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

