If you’ve ever shuffled a deck of playing cards, you’ve most likely created a unique deck. That is, you’re probably the only person who has ever arranged the cards in precisely that order. Although this claim sounds incredible, it’s a great illustration of how quickly large numbers can creep into everyday situations—with occasionally challenging consequences, as the developers of an online poker game painfully discovered in the late 1990s.
The mathematics of card shuffling is quite easy to explain. To calculate how many arrangements 52 playing cards can have, you must go through all the possible shuffles. So logically, one of the 52 cards is placed on top, and once that’s determined, there are only 51 possibilities for the card below it. The next card has only 50 possible options, and so on. A 52-card deck can therefore be arranged in 52 × 51 × 50 × … × 2 × 1 = 52! different ways.
If you do the multiplication and round the answer, you will get a number with 67 zeros. That’s more than a quadrillion times as many ways to arrange these cards as there are atoms on Earth.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
So clearly there are many, many different ways to arrange 52 playing cards. And yet to find out how likely it is that another person in the world will randomly create the same sequence of cards by shuffling, it’s not enough to simply calculate 1 / 52! That number simply indicates how likely it is to get one very specific shuffle of cards.
There’s a more subtle question to consider: How likely would it be for any two or more people in the world to randomly shuffle a deck of cards in the same way?
The Extraordinary Rarity of Each and Every Shuffle
This question is reminiscent of the birthday paradox. It works according to the same principle: It is rather unlikely that a student in a class has a birthday on a given date—in a group of 30 people, the probability of this is 1 − (364 / 365)30≈ 7.9 percent. The probability that two students are born on the same day is more than 70 percent, however. The reason for this apparent discrepancy is that people usually underestimate how many possible pairs of students there are. From 30 students, 435 pairs can be formed. The probability that each pair of students was born on a different day then doesn’t seem so high.
If you want to find out how likely it is to randomly shuffle a deck of cards in the same way as any other person in the world, there are several ways to do it. One is to first calculate the probability of the opposite event and then subtract this result from 1. This means that you first examine how likely it is that all people in the world create a completely new arrangement when mixing: the first person has a probability of 1, the second a probability of (52! – 1) / 52!, the third of (52! – 2) / 52!, and so on. Then subtract this result from 1.
If there are eight billion people in the world, the probability that several people create the same shuffle of cards can be calculated as follows:
The trouble is that my calculator (or rather, the online program Wolfram|Alpha) fails when I try to evaluate this formula. Therefore, I have to rely on a very rough estimate of this probability:
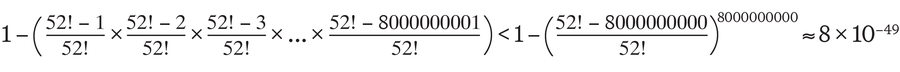
This means that the probability that two or more people in the world will create the same deck of cards is less than 0.0000…08 percent—a number that only deviates from 0 in the 47th decimal place.
With that illustration, I hope I have convinced everyone that it is extremely unlikely that several people in the world would randomly create the same deck of cards by shuffling. But you have probably shuffled cards many times in your life, not just once. So how does the result change if we assume that each person shuffles approximately 100 decks of cards in their lifetime? By replacing the eight billion in the previous estimate with 800 billion, we find that the probability in this case is less than 8 × 10−43 percent.
In other words, the odds don’t change by much. Even if each person in the world shuffles a deck of cards 100 times, it is very unlikely that the same deck will appear twice.
For that matter, if we consider every person who lives or has ever lived on earth—by some estimates, about 117 billion people—each of whom has shuffled a deck of cards about 100 times (which is unlikely, given that our species has not had playing cards for very long), then the probability that the same arrangement was created multiple times is less than 1.7 × 10−40 percent.
This makes it clear: it is truly extremely unlikely that two people in the entire history of humanity have ever shuffled a deck of cards the same way—at least assuming they shuffled the cards with great care. This illustrates how big 52! is and how enormously many possibilities there are for arranging 52 cards.
Read ’Em and Weep
The vastness of 52! is not only inspiring to contemplate—it has also posed some significant practical problems for online game developers. Online poker can involve large sums of money, so it’s critical that these games are as secure and fair as possible. Any flaws or loopholes could be exploited by cheaters or used by the house against players.
Digital cards should be well shuffled and dealt randomly, just like real ones. In an ideal world, an algorithm would randomly select an arrangement from the 52! possible decks. But no computer has enough memory to evaluate all of these possibilities, and a perfect random number generator doesn’t yet exist. Therefore, developers generally rely on algorithms that simulate card shuffling.
In the late 1990s the development platform ASF Software supplied several online poker providers, such as Planet Poker, with card-shuffling algorithms. The platform even posted the algorithm on its website as proof that the game was reliably programmed. And this post caught the attention of some employees at Reliable Software Technologies, an IT company. “As soon as we saw the shuffling algorithm, we began to suspect there might be a problem. A little investigation proved that this intuition was correct,” a few employees wrote in a poston a software development website.
The algorithm started with an ordered deck of cards and then swapped two cards at a time in several steps. To do this, the program used a random number generator linked to the computer’s system time. But there are several constraints on this method. For one, the swapping mechanism was implemented such that certain card arrangements were favored and more likely to appear than others. For another, the system ties its number generation to the number of seconds that have passed since midnight, resetting once each day, which further limits the possible random values. Only about 86 million arrangements could be generated this way, the Reliable Software Technologies team discovered.
The programmers then realized that because the system is tied to a clock to randomize its shuffles, the arrangement of cards could be further constrained by taking that timekeeper into account. Simply syncing up their own program to the system clock reduced the possibilities to a mere 200,000 potential decks that the algorithm could generate. “After that move, the system is ours, since searching through this tiny set of shuffles is trivial and can be done on a PC in real time,” they wrote. Recall that this was back in the 1990s, when computers were significantly less powerful than they are today.
The employees of Reliable Software Technologies reported these weaknesses to the algorithm’s developers, who immediately revised it. Today many online poker sites use the Fisher–Yates algorithm, also called the Knuth shuffle (which sounds delightfully like a dance). It’s easy to implement and delivers satisfactory results.
Of course, these algorithms are constrained in other ways—random generators simply aren’t good enough to do what people can do with an actual deck. But even the most skillful human dealer cannot provide a perfect hand every time.
Thanks to the German language podcast Nerds at Work podcast for inspiring me to write about this 1990s poker algorithm.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

