New Knot Theory Discovery Overturns Long-Held Mathematical Assumption

New Knot Theory Discovery Overturns Long-Held Mathematical Assumption

By Max Springer edited by Sarah Lewin Frasier

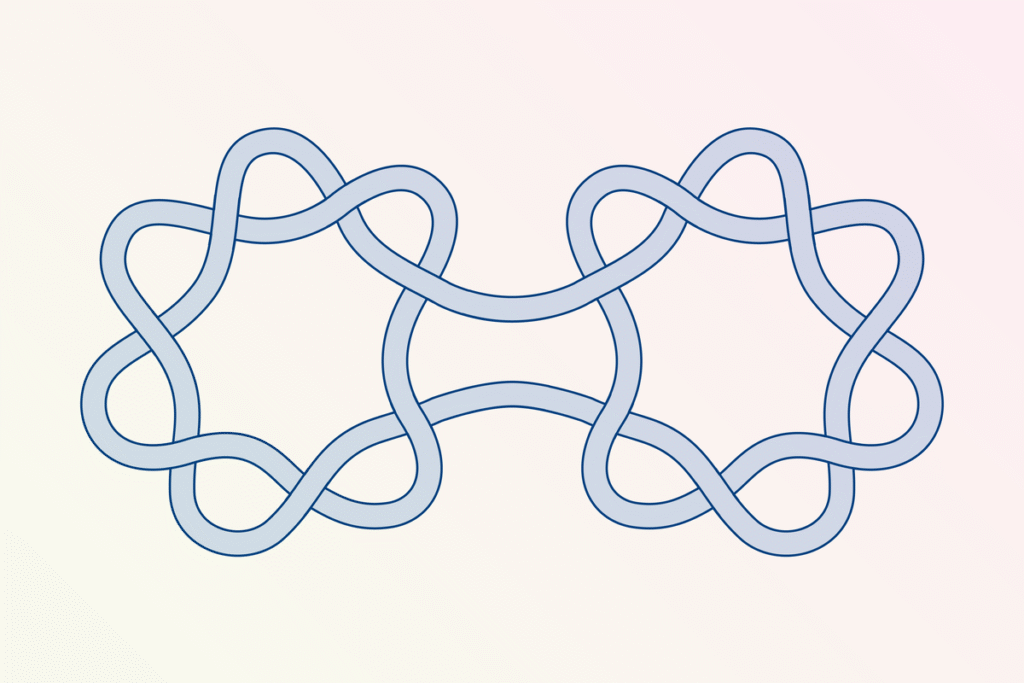
Scanning the crowd at a fancy soiree may reveal a wide array of neckties, each fastened with a highly complex mathematical object masquerading as fashion. An entire field of mathematics is devoted to understanding mathematical knots, which one can obtain from any traditional knot by gluing the loose ends together. Mathematicians long believed that if you attach cut ends of two different knots to each other, the new knot will be just as complex as the sum of the individual knots’ complexity. But researchers recently managed to find a knot that is simpler than the sum of its parts.

Knot theory is a branch of topology that has surprisingly practical applications, such as understanding how proteins coil DNA and how molecular structures remain stable. The theory’s central question: How can we tell which knots are unique or which are the same as others? Mathematicians consider two knots the same if one can be manipulated to look like the other without being cut open—any knots you can produce with mere tugging and pulling are fundamentally the same. Only cutting and reconnecting to let two strands cross yields unique knots.

Using these careful manipulations, mathematicians assign each knot an unknotting number, which is the minimum number of cutting and reconnecting “moves” it would take to unravel the knot into a simple loop. This computation is often deceptively difficult. Many mathematicians assumed that if we construct a larger knot by joining together smaller ones whose unknotting numbers are known, then the quickest way to untangle the larger knot will be by simply undoing each piece independently. This idea that two conjoined knots’ unknotting numbers can be added was first proposed as a conjecture by Hilmar Wendt in a 1937 paper and remained open for nearly a century. Until recently, “there was no clear way to prove this conjecture,” says Mark Brittenham, a mathematician at the University of Nebraska–Lincoln, “and now we know why—because it’s false.”

On supporting science journalism

If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For a preprint paper posted online at arXiv.org, Brittenham and his co-author, Susan Hermiller, a mathematician also at the University of Nebraska–Lincoln, tied two knots that, when connected, require an unexpectedly small number of moves to undo. The mathematicians connected one knot with an unknotting number of three to its mirror image to form a larger knot. Instead of six moves, this “complicated mess of a [knot]” ultimately can be undone with only five maneuvers and possibly even fewer, Hermiller says.

“This is quite surprising,” says Rutgers University mathematician Kristen Hendricks, who was not involved in the study. “The result says that our notions of [knot] complexity could have problems.”

So the next time you’re battling a necktie or complicated scarf, take some comfort in knowing that even the simplest-seeming structures can conceal a world of unexpected mathematical complexity.

It’s Time to Stand Up for Science

If you enjoyed this article, I’d like to ask for your support. Scientific American has served as an advocate for science and industry for 180 years, and right now may be the most critical moment in that two-century history.

I’ve been a Scientific American subscriber since I was 12 years old, and it helped shape the way I look at the world. SciAm always educates and delights me, and inspires a sense of awe for our vast, beautiful universe. I hope it does that for you, too.

If you subscribe to Scientific American, you help ensure that our coverage is centered on meaningful research and discovery; that we have the resources to report on the decisions that threaten labs across the U.S.; and that we support both budding and working scientists at a time when the value of science itself too often goes unrecognized.

In return, you get essential news, captivating podcasts, brilliant infographics, can’t-miss newsletters, must-watch videos, challenging games, and the science world’s best writing and reporting. You can even gift someone a subscription.

There has never been a more important time for us to stand up and show why science matters. I hope you’ll support us in that mission.