What Is the Luhn Algorithm? The Math Behind Secure Credit Card Numbers

The Math Trick Hidden in Your Credit Card Number

By Jack Murtagh edited by Jeanna Bryner

You’re at the checkout screen after an online shopping spree, ready to enter your credit card number. You type it in and instantly see a red error message: “Please enter a valid credit card number.” Annoyed, you scan back through each digit and spot the culprit: you tapped the 6 key where a 5 belonged. Typo corrected; purchase complete. But how did the website detect your error so quickly? Does the online platform keep a master list of every valid credit card number to compare your entry against? Did it ping your bank in a split second? The explanation is much cleverer.

All mainstream credit card numbers obey a mathematical trick designed to catch the most common typos. It’s called the Luhn algorithm, named after IBM researcher Hans Peter Luhn, who patented it in 1960. Similar error-checking schemes lurk in many of the numbers you encounter daily: barcodes, package tracking numbers, bank account numbers and even ISBNs on books.

Grab a credit card from your wallet, and you’ll find it contains more structure than first glance suggests. The anatomy of a credit card number includes four main parts. To demonstrate, I’ll use my personal Visa. [Stretch your math muscles with these puzzles]

On supporting science journalism

If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

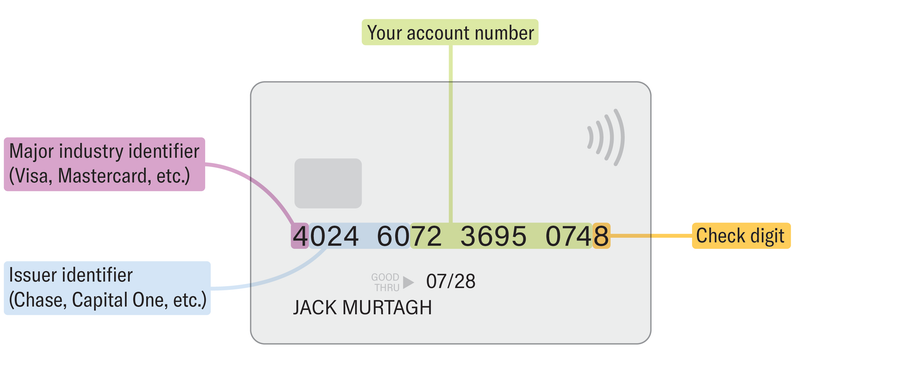
The first digit is the major industry identifier. Visas always begin with a 4, and Discovers always start with a 6. The next five to seven digits pinpoint the bank or institution that issued the card. What remains (sans the final digit) is your specific account number within that bank. The final digit, sometimes called the “check digit,” has nothing to do with financial institutions. Issuers tack it on so that the whole card number will satisfy a specific mathematical test—the Luhn algorithm. Here’s how the algorithm works:

1. Write out all but the last digit of the card number.

2. Double every other number starting at the right.

3. Sum the resulting

   digits (not numbers). E.g., if you doubled a 7 to become a 14 in Step 2, this will become 1 + 4 = 5 in this step.

4. Add the check digit to the sum. If the result is not a multiple of 10, then the credit card number is invalid.

I’ll show the Luhn algorithm in action on my Visa, but you should try it with your credit card, too.

The number crunching culminates in 75, which is not a multiple of 10. So this cannot be my real credit card number; I must have mistyped it.

Credit card issuers first assign the account numbers and then compute steps one through three of the Luhn algorithm to determine the appropriate check digit. In this case, the card number should have ended in a 3 because 67 + 3 = 70, a multiple of 10.

This particular dance of digits has come to dominate credit card verification because of its simplicity and powerful set of features. If you mess up any single digit when entering your card number, the Luhn algorithm will detect it. If you accidentally swap adjacent card digits while inputting, it will detect that, too (with the one exception of flipping 09 to 90, or vice versa).

Dutch mathematician Jacobus Verhoeff reported in 1969 that two errors—mistyping a single digit and swapping two neighboring digits of one’s card number—account for nearly 90 percent of all human input errors in practice. Verhoeff developed an even more comprehensive algorithm that, in addition to detecting all of the same typos as Luhn’s algorithm, also catches 09/90 transpositions, as well as more exotic slipups. Verhoeff’s algorithm was a mathematical triumph. Some contemporaries had even published false proofs claiming that no single check digit could carry enough information to catch all of these errors. Verhoeff’s algorithm never gained widespread adoption, however, perhaps because of its increased complexity over Luhn’s or because Luhn’s algorithm was already deployed and did a sufficient job.

Luhn’s algorithm saves you time and businesses money. At some point during a purchase, a vendor will verify that your card belongs to you by sending your information to a specialized card-validation service. This communication takes time and incurs processing fees for the business. It would be a waste of seconds and cents to outsource needless back-and-forth with a professional validation service to catch common typos. Because Luhn’s algorithm requires so little processing power, the computer handling the transaction can also run the check without needing to contact any third party.

Importantly, passing Luhn’s algorithm does not guarantee a valid credit card number. Rather failing it guarantees an invalid credit card number. The algorithm puts up a first line of defense that less common typos and savvy fraudsters can slip through. Those cases get caught by the more resource-intensive card-validation services.

How does Luhn’s algorithm know when your fingers fumble? Every digit in a credit card number contributes a one-digit number to the final sum in the algorithm. If the digit sits in a position that does not get doubled, then it just contributes itself to the sum. But even if a digit sits in a doubled position, summing the individual digits of the resulting two-digit number always yields a one-digit number again. The table below lists all of these possible contributions:

For example, 6 contributes 6 when it’s in an undoubled position and it contributes 3 from a doubled position because 6 doubled equals 12 and 1 + 2 = 3. Messing up a single number while typing your credit card effectively shifts you up or down within the same column of this table and alters one term in the algorithm’s sum. By design, a valid credit card number results in a sum that is a multiple of 10. Any single-digit error will change the sum by a one-digit number, so the mistaken sum will definitely not be a multiple of 10.

Formally proving that Luhn’s algorithm detects swapping adjacent digits involves some case analysis, but an example will help illustrate the idea. Imagine we have the sequence 31 in our credit card, with the 3 in a doubled position. We accidentally enter 13 instead. In the correct sum, this duo contributes 6 + 1 = 7 (3 doubled plus 1 undoubled), whereas in the faulty sum, it contributes 2 + 3 = 5 (1 doubled plus 3 undoubled). So the error ultimately changes our sum by 2: going from a contribution of 7 to a contribution of 5. If the original sum yielded a multiple of 10, then there’s no way this new one will. We can check that this works for every pair of numbers except for 09/90, which both contribute the same quantity to the Luhn sum.

Next time a checkout page flashes that annoying error message, remember: a simple piece of math under the hood just saved a little time and money for everyone involved.